What Percentage Of 32 Is 4
Kalali
Apr 25, 2025 · 5 min read
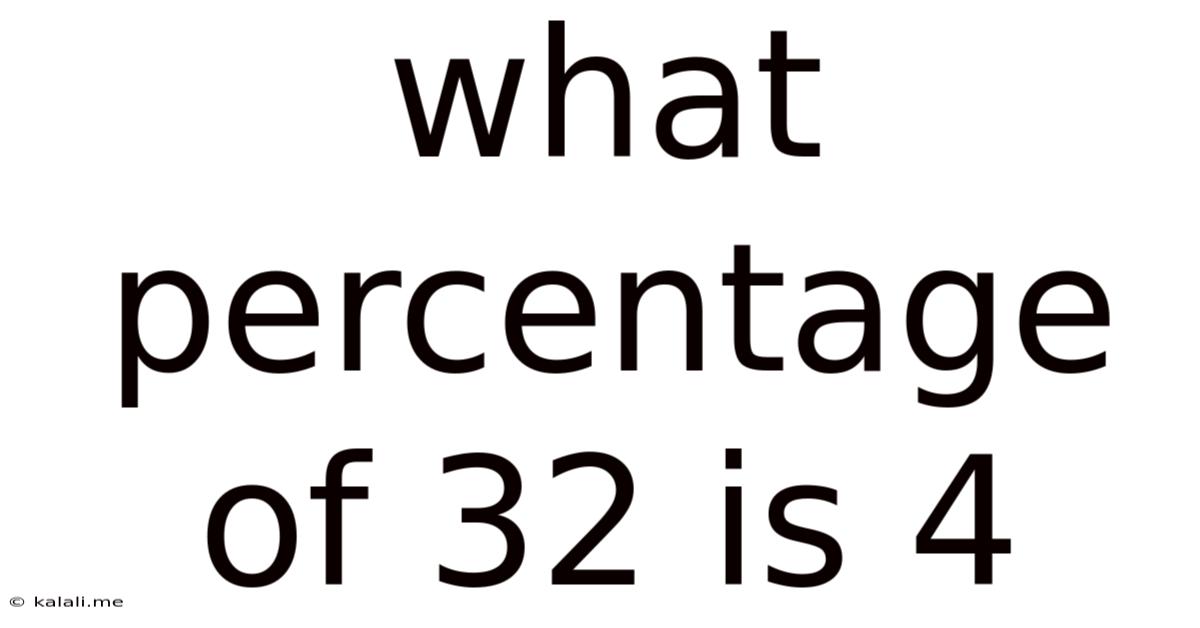
Table of Contents
What Percentage of 32 is 4? A Deep Dive into Percentage Calculations
This article will explore the seemingly simple question: "What percentage of 32 is 4?" While the answer might seem immediately obvious to some, we'll delve into the underlying mathematical principles, explore different methods for solving this type of problem, and discuss the broader applications of percentage calculations in everyday life and various fields. Understanding percentages is crucial for everything from budgeting and finance to data analysis and scientific research. This comprehensive guide will equip you with the knowledge and skills to confidently tackle percentage problems of all complexities.
Understanding Percentages: A Foundation
A percentage is a way of expressing a number as a fraction of 100. The symbol "%" represents "per cent," meaning "out of one hundred." Therefore, 10% means 10 out of 100, which can also be expressed as the fraction 10/100 or the decimal 0.10. Percentages are used to represent proportions, rates, and changes in a way that's easily understandable and comparable.
Method 1: Using the Percentage Formula
The most common and straightforward method for determining what percentage one number is of another is using the basic percentage formula:
(Part / Whole) x 100% = Percentage
In our problem, "What percentage of 32 is 4?", we identify:
- Part: 4 (the number we want to express as a percentage)
- Whole: 32 (the total number)
Plugging these values into the formula:
(4 / 32) x 100% = 0.125 x 100% = 12.5%
Therefore, 4 is 12.5% of 32.
Method 2: Using Proportions
Another approach involves setting up a proportion. A proportion is an equation stating that two ratios are equal. We can set up a proportion to solve our problem as follows:
4 / 32 = x / 100
Where 'x' represents the percentage we're trying to find. To solve for 'x', we cross-multiply:
32x = 400
x = 400 / 32
x = 12.5
Thus, again, we find that 4 is 12.5% of 32.
Method 3: Using Decimal Conversion
We can also solve this by first converting the fraction to a decimal and then multiplying by 100%:
4 / 32 = 0.125
0.125 x 100% = 12.5%
This method highlights the direct relationship between fractions, decimals, and percentages.
Practical Applications of Percentage Calculations
Understanding percentage calculations is fundamental in numerous areas of life:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns all rely heavily on percentage calculations. For example, understanding the percentage increase or decrease in your savings account balance is crucial for financial planning. Similarly, calculating the percentage of your income allocated to different expenses is vital for budgeting and managing finances effectively.
-
Data Analysis: Percentages are indispensable in interpreting data, representing proportions within datasets, and comparing different groups. In market research, for instance, percentages are used to represent market share, consumer preferences, and satisfaction levels. Data scientists utilize percentages to analyze trends, identify patterns, and draw meaningful conclusions from large datasets.
-
Science: Percentage calculations are critical in scientific research for various applications, including expressing concentrations of solutions, measuring reaction yields, and analyzing experimental data. For example, determining the percentage of a specific element in a compound is essential in chemistry. In biology, percentages are frequently used to represent population growth or decline rates.
-
Everyday Life: We encounter percentages in everyday situations, such as calculating tips in restaurants, determining sale prices in stores, understanding nutritional information on food labels, and interpreting statistics reported in news articles. For example, understanding the percentage of fat or sugar in a food product allows for informed dietary choices.
Beyond the Basics: More Complex Percentage Problems
While the problem "What percentage of 32 is 4?" is relatively simple, percentage calculations can become significantly more complex. Here are a few examples of more challenging scenarios:
-
Finding the Whole: If you know that 15% of a number is 6, how do you find the original number? This requires rearranging the percentage formula to solve for the "Whole."
-
Finding the Part: If 20% of a number is 10, what is 30% of the same number? This involves finding the "Whole" first and then calculating the required percentage.
-
Percentage Change: Calculating percentage increase or decrease is crucial for comparing values over time. For example, understanding the percentage change in sales revenue from one year to the next is crucial for business analysis. This involves calculating the difference between two values and expressing that difference as a percentage of the original value.
-
Compound Interest: Compound interest involves earning interest on both the principal amount and accumulated interest from previous periods. This requires understanding exponential growth calculations, which build upon the fundamental principles of percentages.
Mastering Percentage Calculations: Tips and Tricks
-
Practice Regularly: The best way to master percentage calculations is to practice regularly. Solve a variety of problems to build confidence and fluency.
-
Use Different Methods: Experiment with different approaches (formula, proportion, decimal conversion) to find the method that works best for you.
-
Understand the Concepts: Focus on understanding the underlying mathematical concepts rather than just memorizing formulas.
-
Check Your Work: Always double-check your calculations to ensure accuracy. Use estimation to verify the reasonableness of your answers.
-
Utilize Online Resources: There are numerous online resources, including calculators and tutorials, that can assist you in learning and practicing percentage calculations.
Conclusion: The Importance of Percentage Understanding
The seemingly simple question, "What percentage of 32 is 4?" serves as a gateway to understanding a fundamental mathematical concept with far-reaching applications. Mastering percentage calculations is essential for navigating various aspects of life, from personal finance and data analysis to scientific research and everyday decision-making. By understanding the underlying principles and practicing regularly, you can build confidence and proficiency in this crucial skill. This ability to accurately and efficiently calculate percentages empowers you to analyze data, interpret information, and make informed decisions across a broad spectrum of contexts. Remember that consistent practice and a thorough understanding of the underlying concepts are key to mastering percentage calculations.
Latest Posts
Latest Posts
-
24 Celsius Equals What In Fahrenheit
Apr 26, 2025
-
How Much Is 41 Inches In Feet
Apr 26, 2025
-
Thousands Of An Inch To Mm
Apr 26, 2025
-
How Many Inches Is 4 6 Cm
Apr 26, 2025
-
10 Is What Percent Of 30
Apr 26, 2025
Related Post
Thank you for visiting our website which covers about What Percentage Of 32 Is 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.