What Percentage Of 40 Is 30
Kalali
Mar 26, 2025 · 4 min read
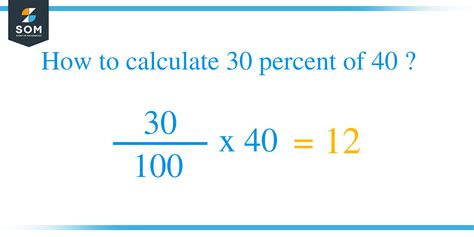
Table of Contents
What Percentage of 40 is 30? A Deep Dive into Percentage Calculations
Finding what percentage one number represents of another is a fundamental skill in mathematics, with applications spanning various fields from finance and statistics to everyday life. This article will comprehensively explore how to calculate what percentage 30 represents of 40, offering multiple approaches and delving into the underlying concepts. We’ll also discuss practical applications and explore related percentage problems.
Understanding Percentages
Before diving into the calculation, let's solidify our understanding of percentages. A percentage is a fraction expressed as a number out of 100. The symbol "%" signifies "per hundred" or "out of 100". For example, 50% means 50 out of 100, which is equivalent to the fraction ½ or the decimal 0.5.
Method 1: Using the Percentage Formula
The most straightforward method to determine what percentage 30 is of 40 is by employing the basic percentage formula:
(Part / Whole) x 100% = Percentage
In our case:
- Part: 30 (the number we want to express as a percentage)
- Whole: 40 (the total number)
Substituting these values into the formula:
(30 / 40) x 100% = 75%
Therefore, 30 is 75% of 40.
Method 2: Simplifying the Fraction
We can simplify the fraction 30/40 before multiplying by 100%. Both the numerator (30) and the denominator (40) are divisible by 10:
30/40 simplifies to 3/4
Now, we convert the simplified fraction into a percentage:
(3/4) x 100% = 75%
This method demonstrates that simplifying fractions can make percentage calculations easier and faster.
Method 3: Using Proportions
Another approach involves setting up a proportion:
30/40 = x/100
Here, 'x' represents the percentage we want to find. To solve for x, we cross-multiply:
40x = 3000
x = 3000 / 40
x = 75
Therefore, x = 75%. This method highlights the relationship between fractions and proportions in percentage calculations.
Practical Applications of Percentage Calculations
Understanding percentage calculations is crucial in various real-world scenarios:
-
Finance: Calculating interest rates, discounts, profit margins, tax rates, and investment returns all rely heavily on percentage calculations. For example, if a bank offers a 5% interest rate on a savings account, calculating the actual interest earned requires understanding percentages.
-
Statistics: Percentages are widely used in presenting statistical data, such as survey results, population demographics, and economic indicators. Understanding percentages allows for effective interpretation and comparison of these data.
-
Sales and Marketing: Discounts, sales tax, and markups are all expressed as percentages. Businesses use these calculations to determine pricing strategies, track sales performance, and analyze market trends.
-
Everyday Life: Calculating tips in restaurants, understanding sales discounts, and determining the percentage of a task completed are all common examples of everyday applications of percentage calculations.
Related Percentage Problems and Advanced Techniques
Let's explore some related problems and introduce more advanced techniques:
1. Finding the Whole when the Percentage and Part are Known:
Suppose you know that 25% of a number is 10. How do you find the total number?
We can set up the equation:
0.25x = 10
Solving for x:
x = 10 / 0.25
x = 40
Therefore, the whole number is 40.
2. Finding the Part when the Percentage and Whole are Known:
If you know that 60% of 80 is a certain number, how do you find that number?
We can calculate this directly:
0.60 x 80 = 48
Therefore, 60% of 80 is 48.
3. Percentage Increase and Decrease:
Percentage increase and decrease calculations are common in many applications. For example:
-
Percentage Increase: If a price increases from $50 to $60, the percentage increase is calculated as: [(60-50)/50] x 100% = 20%
-
Percentage Decrease: If a price decreases from $60 to $50, the percentage decrease is calculated as: [(60-50)/60] x 100% = 16.67%
4. Compound Interest:
Compound interest involves earning interest not only on the principal amount but also on the accumulated interest. This requires more complex calculations than simple interest, often involving exponential growth formulas.
Mastering Percentage Calculations: Tips and Tricks
-
Practice Regularly: The more you practice, the more comfortable you’ll become with percentage calculations. Work through various problems, gradually increasing their complexity.
-
Understand the Fundamentals: Ensure you have a strong grasp of fractions, decimals, and basic algebraic principles. These underpin percentage calculations.
-
Use a Calculator: For more complex calculations, a calculator can save time and ensure accuracy. Many calculators have a percentage function that simplifies the process.
-
Break Down Complex Problems: If faced with a complex problem, break it down into smaller, manageable steps. This makes the process less daunting and reduces the risk of errors.
-
Check Your Work: Always double-check your calculations to ensure accuracy. Simple errors can lead to significant inaccuracies in the final result.
Conclusion: The Power of Percentages
Calculating percentages is a fundamental skill with wide-ranging applications. Understanding the different methods, formulas, and techniques discussed in this article will equip you to confidently tackle various percentage problems, whether they arise in finance, statistics, everyday life, or any other field. By mastering these skills, you enhance your analytical abilities and improve your decision-making capabilities in various situations. Remember to practice regularly and apply your knowledge in real-world scenarios to truly internalize the power of percentages.
Latest Posts
Latest Posts
-
Are Alternate Interior Angles Always Congruent
Mar 29, 2025
-
What Percent Of 40 Is 38
Mar 29, 2025
-
10 Is What Percentage Of 30
Mar 29, 2025
-
What Is 14 15 As A Percentage
Mar 29, 2025
-
Diagram Of Photosynthesis And Cellular Respiration
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about What Percentage Of 40 Is 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
