What Percentage Of 45 Is 3
Kalali
Apr 17, 2025 · 5 min read
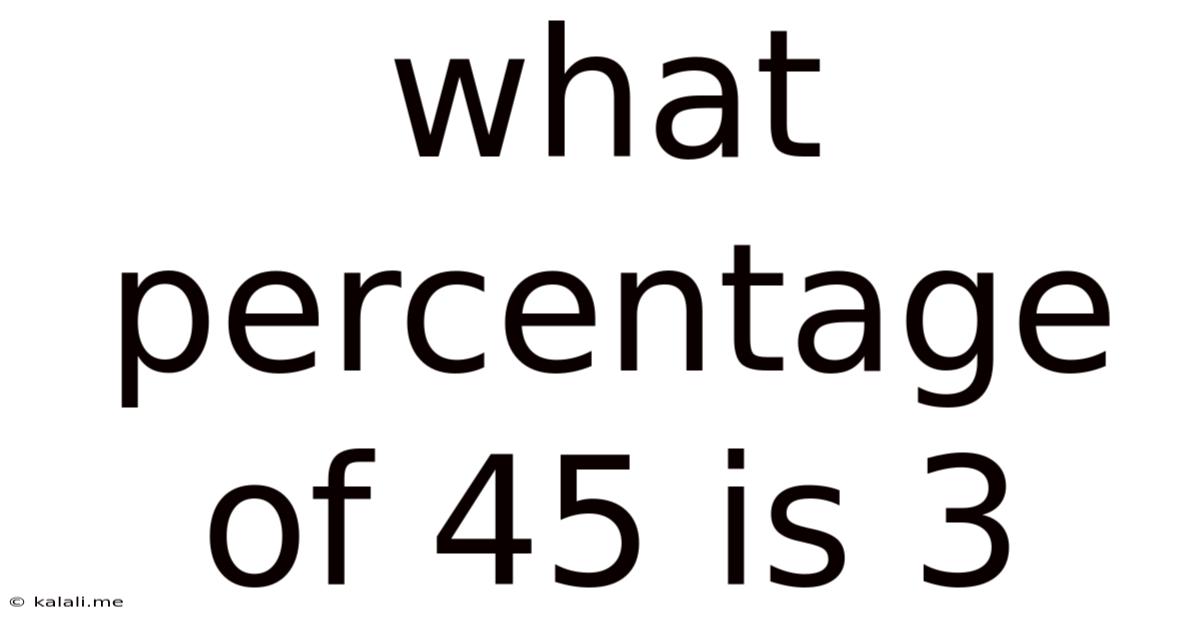
Table of Contents
What Percentage of 45 is 3? A Deep Dive into Percentage Calculations
Finding what percentage one number represents of another is a fundamental skill in mathematics, with applications spanning various fields from finance and statistics to everyday life. This article will thoroughly explore how to calculate what percentage of 45 is 3, providing multiple approaches and explaining the underlying concepts. We'll go beyond the simple calculation and delve into the practical implications and broader understanding of percentage calculations. This will not only answer the question directly but equip you with the tools to solve similar problems with ease.
Meta Description: Learn how to calculate what percentage of 45 is 3. This comprehensive guide explores multiple methods, explains the underlying principles, and provides practical examples for understanding percentage calculations.
Understanding Percentages
Before we tackle the specific problem, let's establish a solid understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" signifies "percent," meaning "out of one hundred." For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5.
Percentages are used extensively to represent proportions, rates, and changes. They offer a standardized way to compare quantities and make relative comparisons easier to understand.
Method 1: Using the Formula
The most direct way to determine what percentage of 45 is 3 is to use the standard percentage formula:
(Part / Whole) x 100% = Percentage
In our case:
- Part: 3 (the number we want to express as a percentage of 45)
- Whole: 45 (the total number)
Substituting these values into the formula:
(3 / 45) x 100% = 6.666...%
Therefore, 3 is approximately 6.67% of 45. The recurring decimal is often rounded to two decimal places for practicality.
Method 2: Simplifying the Fraction
An alternative approach involves simplifying the fraction before multiplying by 100%. This can make the calculation easier, especially with larger numbers.
Start by expressing the relationship as a fraction: 3/45
Now, simplify the fraction by finding the greatest common divisor (GCD) of 3 and 45. The GCD of 3 and 45 is 3. Divide both the numerator and denominator by 3:
3 ÷ 3 = 1 45 ÷ 3 = 15
This simplifies the fraction to 1/15. Now, convert this fraction to a percentage:
(1 / 15) x 100% ≈ 6.67%
Method 3: Using Proportions
Another method uses proportions. We can set up a proportion to solve for the unknown percentage (x):
3 / 45 = x / 100
To solve for x, cross-multiply:
45x = 300
Now, divide both sides by 45:
x = 300 / 45 = 6.67%
Understanding the Result: Practical Implications
The result, 6.67%, tells us that 3 represents a relatively small portion of 45. This information could be relevant in numerous contexts. For example:
- Sales: If a company had a sales target of 45 units and sold 3, their sales performance represents only 6.67% of the target.
- Surveys: If 3 out of 45 respondents chose a particular option in a survey, that option received approximately 6.67% of the votes.
- Inventory: If a warehouse has 45 items and 3 are defective, the percentage of defective items is 6.67%.
- Grades: If a test has a total of 45 points and a student scores 3 points, their score represents 6.67% of the total points.
The significance of this percentage depends entirely on the context in which it is applied.
Expanding on Percentage Calculations: Further Applications
Understanding percentage calculations is crucial for various mathematical and real-world applications. Here are some examples:
- Calculating Percentage Increase or Decrease: This involves determining the percentage change between two values. The formula is: [(New Value - Old Value) / Old Value] x 100%.
- Calculating Percentage Markup: Businesses use percentage markup to determine the selling price of a product based on its cost price.
- Calculating Discounts: Discounts are often expressed as percentages. For example, a 20% discount on a $100 item means the customer pays $80.
- Compound Interest: Compound interest calculations heavily rely on percentages to determine the interest earned on an investment over time.
- Statistical Analysis: Percentages are extensively used in statistics to represent proportions and probabilities.
Common Mistakes to Avoid
When calculating percentages, it's easy to make mistakes. Here are some common errors to watch out for:
- Incorrect Order of Operations: Remember to follow the order of operations (PEMDAS/BODMAS). Perform the division before the multiplication.
- Decimal Point Errors: Pay close attention to decimal points when converting fractions to percentages. A misplaced decimal can significantly alter the result.
- Rounding Errors: Rounding too early in the calculation can introduce inaccuracies. It's best to round only at the final stage.
Advanced Percentage Calculations: Dealing with More Complex Scenarios
While the calculation for "what percentage of 45 is 3" is straightforward, percentage calculations can become more complex. Consider these scenarios:
- Calculating percentages of percentages: This involves calculating a percentage of a percentage, often encountered in compound interest or discounts.
- Working with multiple percentages: Situations might involve applying multiple percentages successively, requiring careful step-by-step calculations.
- Inverse Percentage Problems: These involve finding the original value when a percentage and the resulting value are known.
Conclusion
Calculating what percentage of 45 is 3 is a simple yet fundamental application of percentage calculations. Understanding the different methods, from the basic formula to using proportions, provides flexibility and a deeper understanding of the underlying principles. The ability to perform such calculations efficiently is a valuable skill applicable across numerous fields and everyday situations. Mastering percentage calculations is a cornerstone of numerical literacy and opens doors to more advanced mathematical concepts. By practicing these methods and understanding the potential pitfalls, you can confidently tackle a wide range of percentage problems with accuracy and precision.
Latest Posts
Latest Posts
-
9 As A Percentage Of 25
Apr 19, 2025
-
What Is 1 12 In A Decimal
Apr 19, 2025
-
Cuanto Es 39 Fahrenheit En Celsius
Apr 19, 2025
-
3 6 Amino Acids Per One Alpha Helix Turn
Apr 19, 2025
-
Is The Sun Biotic Or Abiotic
Apr 19, 2025
Related Post
Thank you for visiting our website which covers about What Percentage Of 45 Is 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.