What Percentage Of 7 Is 3
Kalali
Apr 26, 2025 · 5 min read
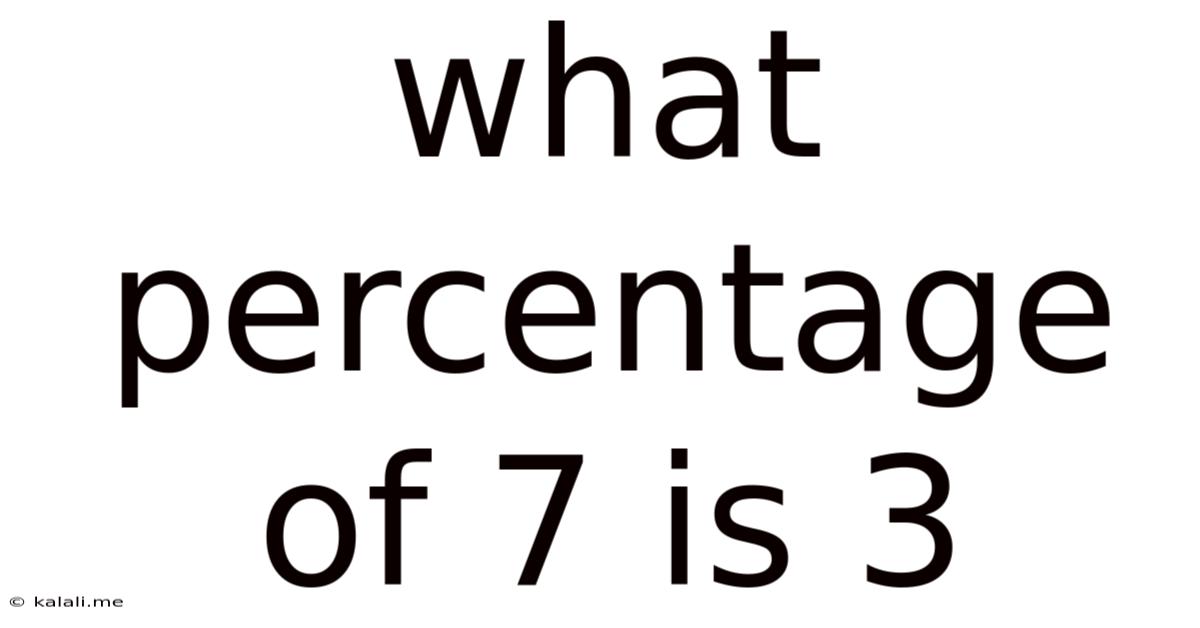
Table of Contents
What Percentage of 7 is 3? Understanding Percentages and Their Applications
This seemingly simple question, "What percentage of 7 is 3?", opens the door to a deeper understanding of percentages, a fundamental concept in mathematics with widespread applications in everyday life and various fields. This article will not only answer the question directly but also delve into the underlying principles, explore different methods of solving percentage problems, and illustrate the practical relevance of percentage calculations. Understanding percentages is crucial for interpreting data, making informed decisions, and navigating the financial aspects of life.
Understanding the Fundamentals of Percentages
A percentage is a way of expressing a number as a fraction of 100. The word "percent" itself derives from the Latin "per centum," meaning "out of a hundred." Therefore, a percentage represents a portion or proportion of a whole, where the whole is always considered to be 100%. For example, 50% represents 50 out of 100, or 50/100, which simplifies to 1/2.
Calculating "What Percentage of 7 is 3?"
To determine what percentage of 7 is 3, we need to set up a proportion. We can express this as:
3 / 7 = x / 100
Where 'x' represents the unknown percentage we are trying to find. To solve for 'x', we can cross-multiply:
7x = 300
Now, we divide both sides of the equation by 7:
x = 300 / 7
x ≈ 42.86
Therefore, 3 is approximately 42.86% of 7.
Alternative Methods for Calculating Percentages
While the proportion method is a classic approach, several other methods can be used to calculate percentages. Let's explore a couple of them:
1. Using Decimal Conversion:
This method involves converting the fraction to a decimal and then multiplying by 100%. First, we represent the problem as a fraction:
3/7
Now, we divide 3 by 7:
3 ÷ 7 ≈ 0.4286
Finally, we multiply the decimal by 100%:
0.4286 × 100% ≈ 42.86%
2. Using a Calculator:
Most calculators have a percentage function. The process is straightforward:
- Divide 3 by 7 (3 ÷ 7).
- Multiply the result by 100.
- The answer will be displayed as a percentage.
Real-World Applications of Percentage Calculations
Percentages are ubiquitous in various aspects of daily life and professional settings. Here are some examples:
1. Finance and Budgeting:
- Interest rates: Banks and financial institutions use percentages to express interest rates on loans, savings accounts, and credit cards. Understanding percentage calculations is vital for comparing different financial products and making informed decisions.
- Discounts and sales: Retailers frequently offer discounts expressed as percentages. Calculating the final price after a discount involves subtracting the percentage discount from the original price. For instance, a 20% discount on a $100 item means a savings of $20, resulting in a final price of $80.
- Taxes: Sales tax, income tax, and property tax are typically expressed as percentages of the taxable amount. Calculating the tax amount involves multiplying the taxable amount by the tax rate.
- Investment returns: Investors track the performance of their investments using percentage returns. A positive percentage return indicates a profit, while a negative percentage return indicates a loss.
2. Data Analysis and Statistics:
- Representing proportions: Percentages are commonly used to represent proportions within a data set. For example, in a survey, percentages can illustrate the proportion of respondents who favor a particular opinion or product.
- Analyzing trends: Percentages are used to analyze trends and changes over time. For instance, comparing sales figures from one year to the next using percentage growth or decline provides valuable insights into business performance.
3. Science and Engineering:
- Measurement errors: Scientists and engineers use percentages to express measurement errors and uncertainties. This helps determine the reliability and accuracy of experimental results.
- Efficiency and productivity: Percentages are used to measure the efficiency and productivity of systems and processes. For instance, the efficiency of a machine can be expressed as a percentage of its theoretical maximum output.
4. Everyday Life:
- Tips and gratuities: Calculating tips in restaurants and other service industries often involves using percentages. A common tip is 15% or 20% of the total bill.
- Sales tax calculations: Consumers often need to calculate the sales tax amount added to their purchases.
Expanding the Understanding of Percentage Problems
The "what percentage of 7 is 3?" question can be expanded to explore more complex percentage problems. For instance:
- Finding a percentage of a number: This involves multiplying the number by the percentage (expressed as a decimal). For example, finding 25% of 80 involves multiplying 80 by 0.25, resulting in 20.
- Finding the original number given a percentage: This involves setting up an equation and solving for the unknown original number. For example, if 30% of a number is 15, we can set up the equation: 0.30x = 15, and solve for x (x = 50).
- Finding the percentage increase or decrease: This involves calculating the difference between two numbers and expressing it as a percentage of the original number. For example, if a price increases from $50 to $60, the percentage increase is calculated as [(60-50)/50] x 100% = 20%.
Mastering Percentage Calculations: Tips and Practice
Mastering percentage calculations requires consistent practice and a solid understanding of the underlying principles. Here are some tips to improve your skills:
- Practice regularly: Solve various percentage problems to build your confidence and fluency.
- Use different methods: Experiment with different approaches to solve problems and find the method that works best for you.
- Check your answers: Always verify your answers using a different method or calculator to ensure accuracy.
- Visualize the problem: Representing the problem visually using diagrams or charts can help improve understanding.
- Break down complex problems: Decompose complex problems into smaller, manageable steps.
- Use online resources: Numerous online resources, including interactive calculators and tutorials, can assist in learning and practicing percentage calculations.
In conclusion, answering the question "What percentage of 7 is 3?" is not merely about obtaining the numerical answer (approximately 42.86%). It is about understanding the fundamental concepts of percentages, mastering various calculation methods, and appreciating the broad applicability of this mathematical concept in numerous facets of life. By practicing and applying these principles, you can effectively utilize percentages to analyze data, make informed decisions, and navigate the quantitative aspects of the world around you.
Latest Posts
Latest Posts
-
What Is 4 7 As A Percentage
Apr 26, 2025
-
What Is The Percentage Of 0 7
Apr 26, 2025
-
What Is 97 Cm In Inches
Apr 26, 2025
-
The Combining Form Vas O Means
Apr 26, 2025
-
37 Degrees Celsius Is What Fahrenheit
Apr 26, 2025
Related Post
Thank you for visiting our website which covers about What Percentage Of 7 Is 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.