Whats 10 To The Power Of 4
Kalali
Aug 26, 2025 · 5 min read
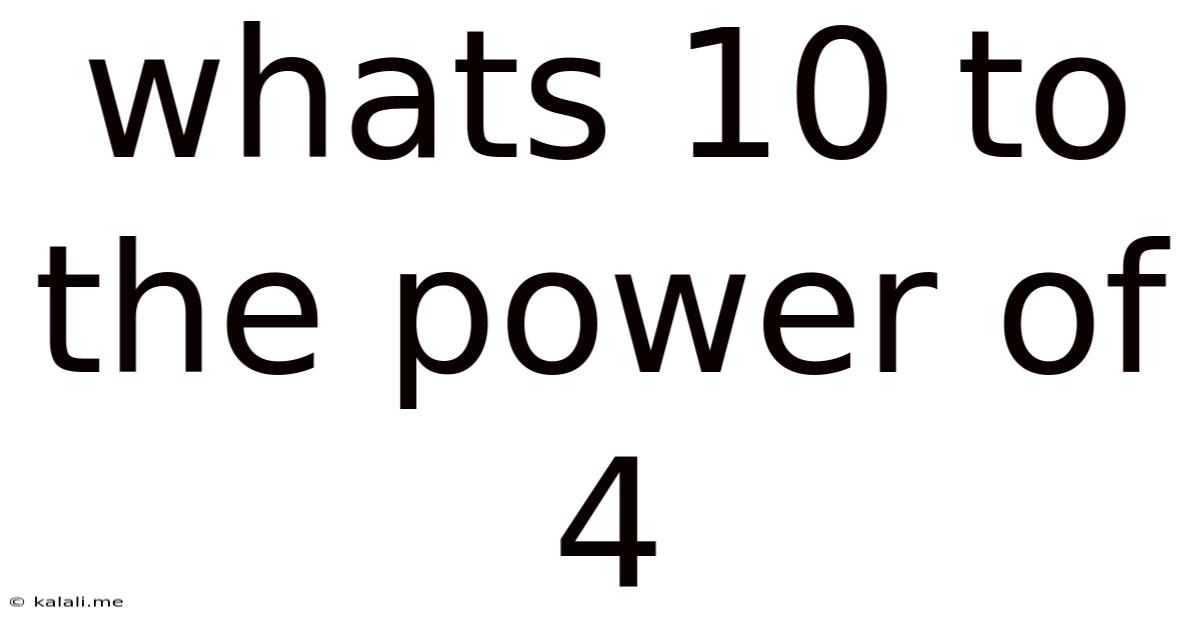
Table of Contents
What's 10 to the Power of 4? A Deep Dive into Exponents and Their Applications
What is 10 to the power of 4? The simple answer is 10,000. But this seemingly straightforward question opens the door to a fascinating exploration of exponents, their mathematical properties, and their widespread applications across numerous fields. This article will not only answer the initial question but delve into the broader context of exponential notation, its practical uses, and related mathematical concepts.
Meta Description: Learn the answer to "What's 10 to the power of 4?" and delve into the world of exponents. Explore their mathematical properties, practical applications in science, technology, finance, and more, with clear examples and explanations.
Understanding Exponents: The Basics
Before we dive into the specifics of 10 to the power of 4, let's establish a fundamental understanding of exponents. An exponent, also known as a power or index, indicates how many times a number (the base) is multiplied by itself. It's written as a superscript number to the right of the base. For example, in the expression 10⁴, 10 is the base and 4 is the exponent. This means 10 is multiplied by itself four times: 10 x 10 x 10 x 10.
The general form is bⁿ, where 'b' represents the base and 'n' represents the exponent. This expression reads as "b to the power of n" or "b raised to the power of n".
Calculating 10 to the Power of 4
Now, let's address the main question: What's 10 to the power of 4 (10⁴)?
As we've established, this means 10 multiplied by itself four times:
10 x 10 x 10 x 10 = 10,000
Therefore, 10 to the power of 4 equals 10,000.
Expanding the Understanding: Powers of 10
Powers of 10 are particularly important because they form the basis of our decimal number system. Understanding these powers allows us to easily work with large and small numbers using scientific notation. Let's explore some examples:
- 10⁰ = 1: Any number raised to the power of zero is equal to 1.
- 10¹ = 10: The first power of any number is simply the number itself.
- 10² = 100: This is ten squared, or 10 multiplied by itself twice.
- 10³ = 1000: This is ten cubed, or 10 multiplied by itself three times.
- 10⁴ = 10,000: This is our original question, and we've already established this equals 10,000.
- 10⁵ = 100,000: Ten to the power of five equals 100,000.
- 10⁶ = 1,000,000: Ten to the power of six equals one million.
Notice the pattern: The exponent represents the number of zeros following the 1.
Negative Exponents: Exploring the Reciprocal
The concept of exponents extends beyond positive whole numbers. Negative exponents represent the reciprocal of the base raised to the positive power. For instance:
- 10⁻¹ = 0.1: This is the reciprocal of 10¹, which is 1/10.
- 10⁻² = 0.01: This is the reciprocal of 10², which is 1/100.
- 10⁻³ = 0.001: This is the reciprocal of 10³, which is 1/1000.
In essence, negative exponents represent fractions with a denominator that's a power of 10.
Fractional Exponents and Roots
Exponents can also be fractions. A fractional exponent represents a root. For example:
- 10^(1/2) = √10 ≈ 3.162: This is the square root of 10.
- 10^(1/3) = ³√10 ≈ 2.154: This is the cube root of 10.
- 10^(2/3) = (³√10)² ≈ 4.642: This is the square of the cube root of 10.
In general, b^(m/n) = n√(bᵐ), where 'm' and 'n' are integers.
Applications of Exponents and Powers of 10
The concept of exponents, particularly powers of 10, has vast applications across numerous fields:
-
Scientific Notation: Scientific notation uses powers of 10 to represent very large or very small numbers concisely. For example, the speed of light is approximately 3 x 10⁸ meters per second. This is much easier to write and comprehend than 300,000,000.
-
Computer Science: Binary numbers (base-2) are fundamental in computing, and understanding exponents helps in converting between binary and decimal systems. The capacity of computer memory and storage devices is often expressed using powers of 2 (e.g., kilobytes, megabytes, gigabytes).
-
Finance: Compound interest calculations heavily rely on exponential functions. Understanding exponential growth is crucial for comprehending investments, loans, and other financial instruments.
-
Physics: Many physical phenomena, such as radioactive decay and population growth, are modeled using exponential functions. Understanding exponents is crucial for analyzing these processes.
-
Engineering: Exponents are used extensively in engineering calculations, particularly those involving scaling, power, and signal processing.
-
Chemistry: Concentrations of solutions and reaction rates often involve exponential relationships.
-
Biology: Population growth and decay in biological systems are frequently modeled using exponential functions.
Expanding on 10,000: Real-World Examples
Let's look at some real-world scenarios where 10,000 (10⁴) might appear:
- Population: A small town might have a population of around 10,000 people.
- Finance: An investment could grow to be worth 10,000 dollars after a certain period.
- Measurement: An area could measure 10,000 square meters.
- Data: A dataset might contain 10,000 data points.
Beyond the Basics: Laws of Exponents
Understanding the laws of exponents is essential for manipulating and simplifying expressions containing exponents. These laws include:
- Product Rule: bᵐ x bⁿ = b^(m+n) (When multiplying bases with the same exponent, add the exponents)
- Quotient Rule: bᵐ / bⁿ = b^(m-n) (When dividing bases with the same exponent, subtract the exponents)
- Power Rule: (bᵐ)ⁿ = b^(m x n) (When raising a power to a power, multiply the exponents)
- Zero Exponent Rule: b⁰ = 1 (Any base raised to the power of zero equals 1)
- Negative Exponent Rule: b⁻ⁿ = 1/bⁿ (A negative exponent represents the reciprocal)
Conclusion: The Power of Understanding Exponents
While the answer to "What's 10 to the power of 4?" is simply 10,000, the question itself serves as a springboard for a much deeper understanding of exponents and their significance. From the foundations of our number system to complex scientific and financial models, exponents are an integral part of mathematics and its applications in numerous fields. Mastering the concepts discussed here will not only enhance your mathematical abilities but also provide you with valuable tools for navigating a world increasingly reliant on quantitative analysis. The seemingly simple calculation of 10⁴ opens a door to a vast and fascinating world of mathematical exploration.
Latest Posts
Latest Posts
-
Least Common Multiple Of 18 And 30
Aug 26, 2025
-
What Is 1 1 2 Cups Divided By 4
Aug 26, 2025
-
Is Adam Levine Related To Avril Lavigne
Aug 26, 2025
-
How Many Angles Does A Cube Have
Aug 26, 2025
-
How High Is A 3 Story House
Aug 26, 2025
Related Post
Thank you for visiting our website which covers about Whats 10 To The Power Of 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.