Which Postulate Proves The Two Triangles Are Congruent
Kalali
Mar 27, 2025 · 6 min read
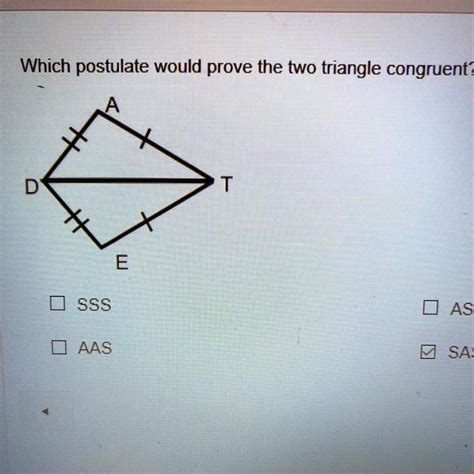
Table of Contents
Which Postulate Proves the Two Triangles are Congruent?
Determining triangle congruence is a fundamental concept in geometry. Understanding the postulates that prove congruence is crucial for solving geometric problems and building a strong foundation in mathematics. This comprehensive guide will delve into the five postulates – SSS, SAS, ASA, AAS, and HL – explaining each one in detail, providing examples, and highlighting their applications. We'll also explore scenarios where these postulates don't apply and discuss the implications.
The Five Postulates of Triangle Congruence
Five postulates underpin the proof of triangle congruence. These postulates provide the necessary conditions to definitively state that two triangles are congruent, meaning they have the same size and shape. Let's examine each one individually:
1. Side-Side-Side (SSS) Postulate
The SSS postulate states that if three sides of one triangle are congruent to three corresponding sides of another triangle, then the two triangles are congruent. This is arguably the most intuitive postulate. Imagine constructing a triangle; if you know the lengths of all three sides, there's only one possible shape and size the triangle can take.
Example:
Consider triangles ABC and DEF. If AB ≅ DE, BC ≅ EF, and AC ≅ DF, then by the SSS postulate, ΔABC ≅ ΔDEF.
Illustration: (Imagine two triangles, ABC and DEF, drawn side-by-side with corresponding sides clearly marked as congruent.)
2. Side-Angle-Side (SAS) Postulate
The SAS postulate asserts that if two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then the two triangles are congruent. The "included angle" is the angle formed by the two sides in question.
Example:
Consider triangles GHI and JKL. If GH ≅ JK, ∠G ≅ ∠J, and GI ≅ JL, then by the SAS postulate, ΔGHI ≅ ΔJKL. Note that ∠G is the included angle between sides GH and GI.
Illustration: (Imagine two triangles, GHI and JKL, drawn side-by-side with corresponding sides and the included angle clearly marked as congruent.)
3. Angle-Side-Angle (ASA) Postulate
The ASA postulate states that if two angles and the included side of one triangle are congruent to two angles and the included side of another triangle, then the two triangles are congruent. Similar to SAS, the "included side" is the side between the two angles.
Example:
Consider triangles MNO and PQR. If ∠M ≅ ∠P, MN ≅ PQ, and ∠N ≅ ∠Q, then by the ASA postulate, ΔMNO ≅ ΔPQR. MN is the included side between ∠M and ∠N.
Illustration: (Imagine two triangles, MNO and PQR, drawn side-by-side with corresponding angles and the included side clearly marked as congruent.)
4. Angle-Angle-Side (AAS) Postulate
The AAS postulate is a close cousin of ASA. It states that if two angles and a non-included side of one triangle are congruent to two angles and the corresponding non-included side of another triangle, then the two triangles are congruent.
Example:
Consider triangles STU and VWX. If ∠S ≅ ∠V, ∠T ≅ ∠W, and TU ≅ WX, then by the AAS postulate, ΔSTU ≅ ΔVWX. Notice that TU is not the included side between the two congruent angles.
Illustration: (Imagine two triangles, STU and VWX, drawn side-by-side with corresponding angles and the non-included side clearly marked as congruent.)
5. Hypotenuse-Leg (HL) Postulate
The HL postulate is specific to right-angled triangles. It states that if the hypotenuse and a leg of one right-angled triangle are congruent to the hypotenuse and a leg of another right-angled triangle, then the two triangles are congruent. The hypotenuse is the side opposite the right angle, and the leg is one of the other two sides.
Example:
Consider right-angled triangles YZA and BXC, where ∠A and ∠C are right angles. If YZ (hypotenuse) ≅ BC (hypotenuse) and YA (leg) ≅ CX (leg), then by the HL postulate, ΔYZA ≅ ΔBXC.
Illustration: (Imagine two right-angled triangles, YZA and BXC, drawn side-by-side with the hypotenuse and a leg clearly marked as congruent.)
When Postulates Don't Apply: Understanding Limitations
It's crucial to understand the limitations of each postulate. Simply having some congruent parts doesn't automatically guarantee congruence.
-
AAA (Angle-Angle-Angle): Knowing only the angles of two triangles doesn't guarantee congruence. Similar triangles have congruent angles but can be of different sizes.
-
SSA (Side-Side-Angle): This is an ambiguous case. There might be two possible triangles that satisfy the given conditions, or no triangle at all. Therefore, SSA is not a valid postulate for proving congruence.
-
SSS with only two sides: Knowing only two sides is insufficient for proving congruence, even if the included angle is known (this is distinct from SAS, which specifies the included angle).
Understanding these limitations is vital to avoid incorrect conclusions.
Applying Congruence Postulates: Problem Solving
Let's work through a few examples to illustrate how to apply these postulates in practical problem-solving:
Example 1:
Given: In ΔPQR and ΔSTU, PQ = ST, QR = TU, and PR = SU.
Prove: ΔPQR ≅ ΔSTU.
Proof: By the SSS postulate, since all three corresponding sides are congruent, ΔPQR ≅ ΔSTU.
Example 2:
Given: In ΔABC and ΔDEF, AB = DE, ∠A = ∠D, and AC = DF.
Prove: ΔABC ≅ ΔDEF.
Proof: By the SAS postulate, since two sides (AB and AC) and the included angle (∠A) are congruent to their corresponding parts in ΔDEF, ΔABC ≅ ΔDEF.
Example 3:
Given: In right-angled triangles XYZ and ABC, where ∠Y = ∠B = 90°, XY = AB, and XZ = AC.
Prove: ΔXYZ ≅ ΔABC.
Proof: By the HL postulate, since the hypotenuse (XZ) and a leg (XY) are congruent to their corresponding parts in ΔABC, ΔXYZ ≅ ΔABC.
Advanced Applications and Implications
The postulates of triangle congruence are not just theoretical concepts; they have significant applications in various fields:
-
Engineering and Construction: Ensuring structural integrity and stability often relies on precise measurements and the principles of triangle congruence.
-
Surveying and Mapping: Determining distances and angles using triangulation techniques heavily depends on understanding triangle congruence.
-
Computer Graphics and Animation: Creating realistic 3D models and animations involves manipulating triangles, and congruence postulates help maintain consistency and accuracy.
-
Robotics and Kinematics: Precise movements and positioning of robotic arms often require analyzing triangle congruence to optimize efficiency and avoid collisions.
Conclusion
Mastering the five postulates of triangle congruence – SSS, SAS, ASA, AAS, and HL – is fundamental to success in geometry and related fields. Understanding when and how to apply each postulate, along with recognizing the limitations, equips you with the skills to solve complex geometric problems and contribute to diverse applications that rely on precise spatial reasoning. Remember to always carefully analyze the given information to identify the appropriate postulate and construct a rigorous proof. Practice is key to developing a strong understanding of these important concepts.
Latest Posts
Latest Posts
-
What Percent Of 50 Is 10
Mar 30, 2025
-
What Is The Percentage Of 0 75
Mar 30, 2025
-
Is Hydrogen Cyanide Polar Or Nonpolar
Mar 30, 2025
-
What Height Is 54 Inches In Feet
Mar 30, 2025
-
Cuantos Litros De Sangre Tenemos En El Cuerpo
Mar 30, 2025
Related Post
Thank you for visiting our website which covers about Which Postulate Proves The Two Triangles Are Congruent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
