Write 4 1 2 As A Decimal Number
Kalali
Mar 27, 2025 · 5 min read
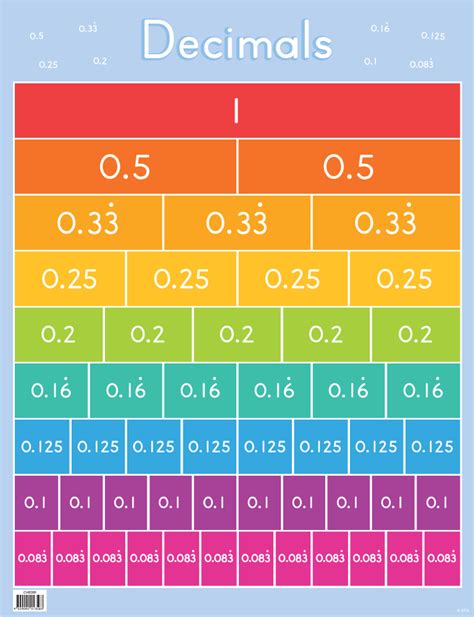
Table of Contents
Writing 4 1/2 as a Decimal Number: A Comprehensive Guide
The seemingly simple task of converting a mixed number like 4 1/2 into its decimal equivalent can be a stepping stone to understanding more complex mathematical concepts. This comprehensive guide will explore multiple methods for this conversion, delve into the underlying principles, and offer practical applications to solidify your understanding. We'll also touch upon the broader context of decimal representation and its importance in various fields.
Understanding Mixed Numbers and Decimals
Before diving into the conversion process, let's define our terms. A mixed number combines a whole number and a fraction, like 4 1/2. A decimal number, on the other hand, uses a base-10 system to represent numbers, employing a decimal point to separate the whole number part from the fractional part (e.g., 4.5). Understanding the relationship between fractions and decimals is crucial for seamless conversion.
The Foundation: Fraction to Decimal Conversion
The core of converting 4 1/2 to a decimal lies in converting the fractional part (1/2) into its decimal equivalent. This involves dividing the numerator (1) by the denominator (2):
1 ÷ 2 = 0.5
This tells us that 1/2 is equal to 0.5. This is a fundamental concept that will be applied to more complex fractions as well.
Method 1: Direct Conversion of the Fractional Part
This method is the most straightforward approach for converting 4 1/2 to a decimal. We already know that 1/2 = 0.5. Since 4 1/2 represents 4 whole units plus 1/2 of a unit, we simply combine the whole number part and the decimal equivalent of the fractional part:
4 + 0.5 = 4.5
Therefore, 4 1/2 as a decimal number is 4.5.
Visualizing the Conversion
Imagine a number line. The whole numbers are clearly marked: 0, 1, 2, 3, 4, 5, and so on. The number 4 1/2 falls exactly halfway between 4 and 5. The decimal representation, 4.5, perfectly reflects this position on the number line, providing a visual confirmation of the conversion.
Method 2: Converting the Mixed Number to an Improper Fraction
This method involves an extra step but offers a more general approach applicable to any mixed number conversion. First, we convert the mixed number 4 1/2 into an improper fraction:
- Multiply the whole number (4) by the denominator of the fraction (2): 4 * 2 = 8
- Add the numerator of the fraction (1) to the result: 8 + 1 = 9
- Keep the same denominator (2): The improper fraction is 9/2
Now, we divide the numerator (9) by the denominator (2):
9 ÷ 2 = 4.5
This confirms that 4 1/2 is equivalent to 4.5 in decimal form.
Advantages of the Improper Fraction Method
While seemingly more complex for this particular example, the improper fraction method provides a structured approach that's highly valuable for converting more intricate mixed numbers. It's especially useful when dealing with fractions that aren't easily converted through simple division, such as 3 7/16 or 2 5/12.
Method 3: Using Decimal Place Value
This method emphasizes the understanding of place value within the decimal system. We already know that the digit to the right of the decimal point represents tenths. In 4 1/2, the fraction 1/2 represents one-half or 0.5 (five-tenths). Therefore, placing this 0.5 after the whole number 4 gives us 4.5.
Understanding Place Value System
The decimal place value system is based on powers of 10. The place immediately to the right of the decimal point is the tenths place (1/10), then the hundredths place (1/100), the thousandths place (1/1000), and so on. Conversely, to the left of the decimal point, we have units, tens, hundreds, and so forth.
Practical Applications of Decimal Conversion
The ability to convert between mixed numbers and decimals is vital in numerous real-world applications:
- Measurement: Many measurements use decimals – for example, 4.5 inches, 4.5 liters, or 4.5 kilograms.
- Finance: Financial calculations often involve decimals representing fractions of currency units (e.g., $4.50).
- Science: Scientific measurements, data analysis, and calculations frequently utilize decimals.
- Engineering: Precision engineering relies heavily on decimal representation for accurate dimensions and calculations.
- Computing: Computers use binary systems, but data is often presented and manipulated using decimal equivalents.
- Cooking and Baking: Recipes frequently involve fractional amounts of ingredients, and understanding decimal equivalents can facilitate precise measurements.
Expanding the Concept: Converting More Complex Mixed Numbers
The principles discussed above are readily applicable to more complex mixed numbers. Let's consider the example of converting 2 3/4 to a decimal:
- Convert the fraction to a decimal: 3 ÷ 4 = 0.75
- Combine with the whole number: 2 + 0.75 = 2.75
Therefore, 2 3/4 is equivalent to 2.75 in decimal form.
Similarly, for the mixed number 5 1/8:
- Convert the fraction to a decimal: 1 ÷ 8 = 0.125
- Combine with the whole number: 5 + 0.125 = 5.125
Thus, 5 1/8 as a decimal is 5.125.
Beyond the Basics: Recurring Decimals
Not all fractions result in terminating decimals. Some fractions produce recurring decimals – decimals where a pattern of digits repeats indefinitely. For example, 1/3 converts to 0.3333... (the digit 3 repeats infinitely). Understanding recurring decimals is crucial for handling more advanced mathematical operations and applications in scientific and engineering fields.
Conclusion: Mastering Decimal Conversion
Converting 4 1/2, or any mixed number, to its decimal equivalent is a fundamental skill in mathematics with widespread applications across various disciplines. By understanding the underlying principles of fraction-to-decimal conversion and utilizing the methods outlined above, you can confidently tackle a wide range of decimal conversion problems. Furthermore, understanding the broader context of the decimal system and its relationship to fractions enhances your overall mathematical literacy and problem-solving capabilities. Remember to practice regularly to solidify your understanding and build your confidence in working with both fractions and decimals.
Latest Posts
Latest Posts
-
What Is The Temperature Of The Asthenosphere
Mar 30, 2025
-
What Is 80 Minutes In Hours
Mar 30, 2025
-
How Many Inches Is 87 Cm
Mar 30, 2025
-
In A Longitudinal Wave The Compressions And Rarefactions Travel In
Mar 30, 2025
-
What Is The Average Atomic Weight Of Silver
Mar 30, 2025
Related Post
Thank you for visiting our website which covers about Write 4 1 2 As A Decimal Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
