X 2 Y 2 Z 4
Kalali
Jun 08, 2025 · 3 min read
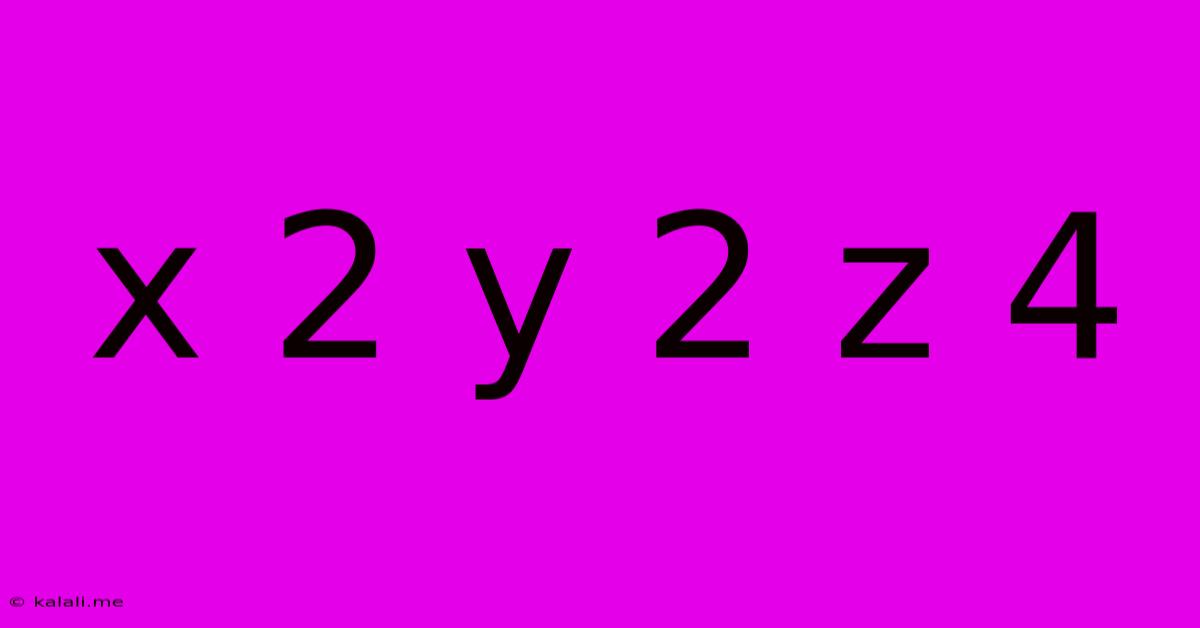
Table of Contents
Exploring the Mathematical Expression: x² + y² + z⁴
This article delves into the mathematical expression x² + y² + z⁴, exploring its properties, potential applications, and its significance within various mathematical contexts. Understanding this seemingly simple equation opens doors to a richer appreciation of algebra, geometry, and even more advanced mathematical fields.
What is x² + y² + z⁴?
At its core, x² + y² + z⁴ is a polynomial expression involving three variables: x, y, and z. Each variable is raised to a different power: x and y are squared (raised to the power of 2), while z is raised to the power of 4. This expression represents the sum of these three terms. The absence of any coefficients (numbers multiplying the variables) implies a coefficient of 1 for each term.
Interpretations and Applications:
While the expression itself is straightforward, its applications are diverse depending on the context:
-
Geometric Interpretation: In three-dimensional space, this expression might represent a surface defined by the equation x² + y² + z⁴ = k, where k is a constant. The shape of this surface would depend on the value of k. For instance, if k is positive, you could potentially visualize it as a warped ellipsoid-like shape. Further analysis involving calculus would be needed for a precise geometric description.
-
Algebraic Manipulation: The expression can be manipulated algebraically using various techniques. For instance, factoring is unlikely to be straightforward given the different powers of the variables. However, substitution methods could simplify the expression in specific scenarios or within larger equations where this expression forms part of a larger algebraic system.
-
Number Theory: If we restrict x, y, and z to integer values, the expression becomes relevant to number theory. Exploring the values this expression can take on for different integer inputs can lead to interesting questions concerning divisibility, prime numbers, and other number theoretic properties. For instance, what are the possible values of x² + y² + z⁴ when x, y, and z are integers? Are there any restrictions on the output values? These are areas of potential exploration.
-
Computer Science: In computational contexts, this expression could appear in algorithms or data structures. It might be used to calculate distances in multi-dimensional spaces or as part of a more complex mathematical model used in simulations or data analysis. The efficiency of calculating this expression for large datasets might also be a topic of interest.
Advanced Considerations:
The expression's complexity increases significantly when dealing with:
-
Complex Numbers: Allowing x, y, and z to be complex numbers opens up a whole new dimension of mathematical possibilities, potentially leading to more intricate geometric interpretations and algebraic solutions.
-
Higher Dimensions: Extending this expression to more variables would lead to generalizations in higher-dimensional spaces. The geometric and algebraic interpretations would become substantially more complex.
Conclusion:
The seemingly simple expression x² + y² + z⁴ offers a fascinating gateway to exploring various areas of mathematics. Its potential applications range from geometric visualization and algebraic manipulation to number theory and computer science. Further investigation into its properties under different mathematical frameworks promises to unveil a wealth of intriguing discoveries. Future research could focus on specific applications or delve deeper into its behavior under diverse constraints and conditions.
Latest Posts
Latest Posts
-
How To Remove Mold From Ceiling In Bathroom
Jun 08, 2025
-
Kill Two Birds With One Stone Alternative
Jun 08, 2025
-
Salesforce User To Create Community User
Jun 08, 2025
-
How To Reset The Rca Tablet
Jun 08, 2025
-
My Wires Dont Match Up To The New Thermostat
Jun 08, 2025
Related Post
Thank you for visiting our website which covers about X 2 Y 2 Z 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.