2 Of 14 Is What Percent
Kalali
Apr 26, 2025 · 5 min read
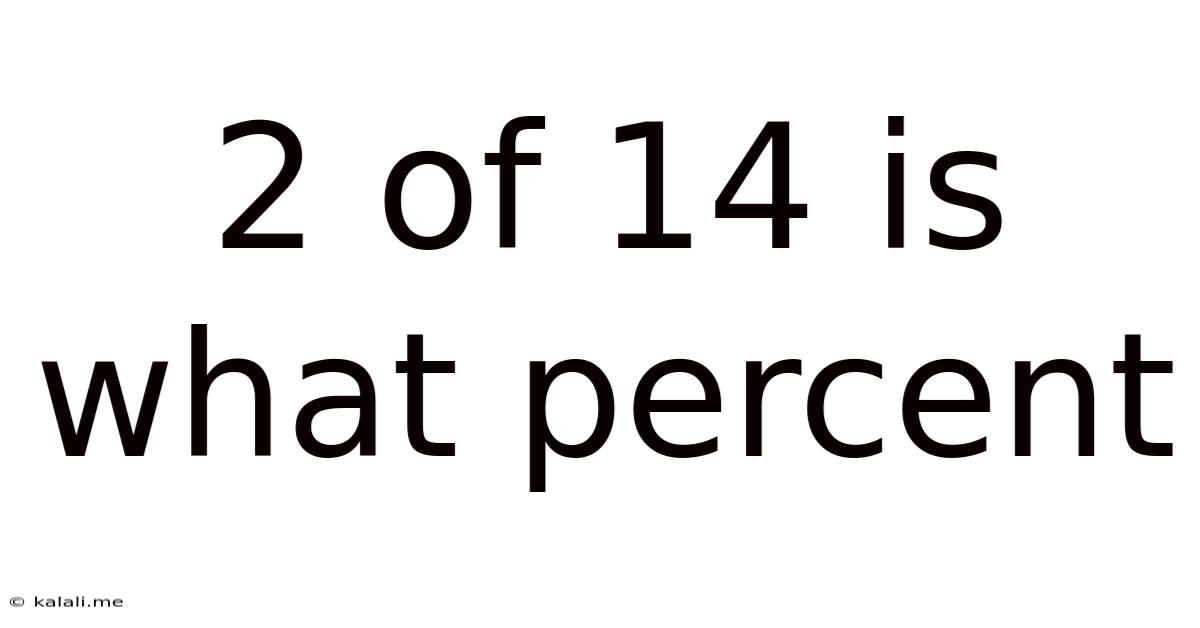
Table of Contents
2 out of 14 is What Percent? A Comprehensive Guide to Percentage Calculations
This seemingly simple question, "2 out of 14 is what percent?", opens the door to a broader understanding of percentages, their applications, and how to calculate them efficiently. This comprehensive guide will not only answer this specific question but also equip you with the knowledge and skills to tackle similar percentage problems with confidence. We'll explore different calculation methods, discuss the importance of percentages in various fields, and delve into some real-world examples to solidify your understanding.
Meta Description: Learn how to calculate percentages effectively! This guide provides a step-by-step explanation of how to determine what percentage 2 out of 14 represents, along with various methods and real-world applications. Master percentage calculations today!
Understanding Percentages
Before diving into the calculation, let's refresh our understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "per cent," which literally means "out of one hundred." So, 50% means 50 out of 100, which is equivalent to ½ or 0.5.
Percentages are incredibly useful for representing proportions, comparing data, and expressing changes or growth. They are widely used in various fields, including finance, statistics, science, and everyday life. Understanding percentages is crucial for making informed decisions and interpreting information accurately.
Calculating "2 out of 14 is What Percent?"
There are several ways to calculate the percentage that 2 out of 14 represents. Let's explore the most common methods:
Method 1: Using Fractions and Decimal Conversion
-
Express as a fraction: The problem "2 out of 14" can be written as the fraction 2/14.
-
Simplify the fraction: To simplify, we find the greatest common divisor (GCD) of 2 and 14, which is 2. Dividing both the numerator and the denominator by 2, we get the simplified fraction 1/7.
-
Convert the fraction to a decimal: To convert 1/7 to a decimal, we divide the numerator (1) by the denominator (7): 1 ÷ 7 ≈ 0.142857
-
Convert the decimal to a percentage: To convert a decimal to a percentage, multiply by 100 and add the "%" symbol: 0.142857 x 100 ≈ 14.29%.
Therefore, 2 out of 14 is approximately 14.29%.
Method 2: Using the Percentage Formula
The basic percentage formula is:
(Part / Whole) x 100% = Percentage
In this case:
- Part = 2
- Whole = 14
Substituting these values into the formula:
(2 / 14) x 100% = 14.29%
This method directly calculates the percentage without the intermediate steps of simplifying fractions and converting decimals.
Method 3: Using a Calculator
Most calculators have a percentage function. Simply enter 2 ÷ 14 and then multiply by 100 to obtain the percentage. This is the quickest method, especially for more complex calculations.
Understanding the Result: 14.29%
The result, 14.29%, indicates that 2 represents approximately 14.29% of the total value of 14. This percentage is relatively small, suggesting that 2 is a minor portion of the whole.
Practical Applications of Percentage Calculations
Percentage calculations are used extensively in various real-world scenarios. Here are a few examples:
-
Finance: Calculating interest rates, discounts, profit margins, tax rates, and investment returns all involve percentage calculations. For instance, understanding compound interest requires a solid grasp of percentages and exponential growth. Calculating a 15% discount on a $100 item involves multiplying 100 by 0.15 to find the discount amount.
-
Statistics: Percentages are vital for representing data in graphs, charts, and tables. They facilitate comparisons between different data sets and aid in the interpretation of statistical findings. For example, comparing the percentage of students who passed a test in different classes helps in evaluating the effectiveness of teaching methods. Similarly, understanding statistical significance often involves working with percentages and probability.
-
Science: In scientific research, percentages are used to express concentrations, error margins, and changes in measured values. For instance, the concentration of a solution is often represented as a percentage. Experimental errors are frequently reported as a percentage of the measured value.
-
Everyday Life: Percentages are used daily in situations such as calculating tips in restaurants, determining sale prices, understanding nutritional information on food labels, or interpreting survey results. Knowing how to compute percentages allows you to make better financial decisions and interpret information more effectively in your daily life.
Further Exploring Percentage Calculations
While we've focused on "2 out of 14 is what percent?", the principles discussed can be applied to any percentage calculation. Here are some additional concepts to explore:
-
Calculating the whole given a percentage and part: If you know that 20% of a number is 10, you can use the formula to determine the whole number.
-
Calculating percentage change: This involves calculating the percentage increase or decrease between two values. The formula for percentage change is:
[(New Value - Old Value) / Old Value] x 100%. This is crucial in tracking changes in various metrics, such as stock prices or population growth. -
Calculating percentage points: It's important to understand the difference between percentage change and percentage points. Percentage points refer to the absolute difference between two percentages. For example, an increase from 10% to 20% is a 10 percentage point increase, but a 100% percentage increase.
-
Compounding percentages: This involves calculating the effect of repeated percentage changes over time. It’s particularly relevant in finance, where understanding compound interest is critical for long-term financial planning.
-
Reverse percentages: These calculations involve finding the original value before a percentage increase or decrease. For instance, if a price increased by 10% to $110, you can use reverse percentage techniques to find the original price.
Conclusion: Mastering Percentage Calculations
The ability to calculate percentages is a fundamental skill with far-reaching applications. Understanding the different methods, from using fractions to applying the percentage formula, enables you to solve a wide array of problems. This guide has not only answered the initial question, "2 out of 14 is what percent?", but has also provided a solid foundation for tackling more complex percentage calculations in various contexts. By mastering these techniques, you'll be better equipped to navigate the world of numbers and make informed decisions in your personal and professional life. Remember to practice regularly, and you'll soon find percentage calculations become second nature.
Latest Posts
Latest Posts
-
What Is The Decimal For 12
Apr 27, 2025
-
9 Is What Percent Of 10
Apr 27, 2025
-
What Does The Acronym Race Stand For In Fire Safety
Apr 27, 2025
-
What Percentage Of 80 Is 10
Apr 27, 2025
-
3 1 2 Quarts To Cups
Apr 27, 2025
Related Post
Thank you for visiting our website which covers about 2 Of 14 Is What Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.