20 Percent Of What Number Is 12
Kalali
Apr 09, 2025 · 5 min read
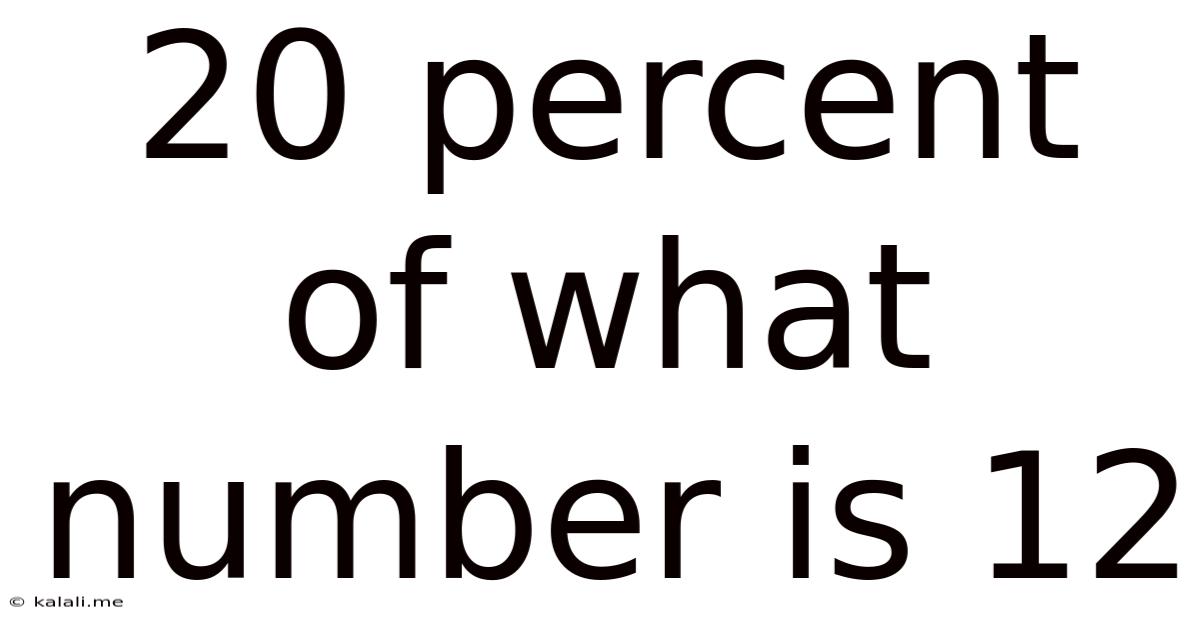
Table of Contents
20% of What Number is 12? Unpacking Percentage Problems and Mastering the Solution
This seemingly simple question, "20% of what number is 12?", actually opens the door to understanding a fundamental concept in mathematics: percentages and their applications in various real-world scenarios. This article will not only provide the solution but also delve into the different methods of solving percentage problems, exploring the underlying principles and offering practical examples to solidify your understanding. We'll cover algebraic approaches, the use of proportions, and even discuss how to tackle more complex percentage problems.
Understanding Percentages: A Quick Refresher
A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per hundred" or "out of 100." For instance, 20% can be written as the fraction 20/100, which simplifies to 1/5 or 0.2 as a decimal. Understanding this basic equivalence is crucial for solving percentage problems.
Method 1: The Algebraic Approach
This is a systematic and widely applicable method for solving percentage problems. Let's represent the unknown number as 'x'. The problem can be translated into an algebraic equation:
0.20 * x = 12
To solve for 'x', we divide both sides of the equation by 0.20:
x = 12 / 0.20
x = 60
Therefore, 20% of 60 is 12.
Method 2: Using Proportions
Proportions offer a visual and intuitive approach to solving percentage problems. We can set up a proportion based on the given information:
20/100 = 12/x
This proportion states that the ratio of 20 to 100 (representing 20%) is equal to the ratio of 12 to the unknown number (x). To solve for 'x', we cross-multiply:
20 * x = 12 * 100
20x = 1200
x = 1200 / 20
x = 60
Again, we find that the unknown number is 60.
Method 3: Working with Decimals
Converting the percentage to a decimal simplifies the calculation. As mentioned earlier, 20% is equivalent to 0.20. So the problem becomes:
0.20 * x = 12
Dividing both sides by 0.20, we get:
x = 12 / 0.20 = 60
This method mirrors the algebraic approach but highlights the direct use of decimal equivalents for percentages.
Expanding on Percentage Problems: Variations and Applications
The basic problem "20% of what number is 12?" serves as a foundation for understanding more complex percentage calculations. Let's explore some variations:
1. Finding the Percentage Increase or Decrease:
Imagine a scenario where a product's price increased by 20% to reach $60. To find the original price, we can use the same principles:
Let x be the original price. The increase is 20% of x, which is 0.20x. The final price is x + 0.20x = 1.20x. Therefore:
1.20x = 60
x = 60 / 1.20 = 50
The original price was $50.
Conversely, if a price decreased by 20% to reach $48, we would solve:
0.80x = 48
x = 48 / 0.80 = 60
The original price was $60. Note that a 20% decrease means the final price represents 80% (100% - 20%) of the original price.
2. Calculating Percentage Change:
Determining the percentage change between two values involves finding the difference between the values, dividing by the original value, and multiplying by 100.
For example, if a value increases from 50 to 60, the percentage change is:
[(60 - 50) / 50] * 100 = 20%
If a value decreases from 60 to 48, the percentage change is:
[(48 - 60) / 60] * 100 = -20%
3. Real-World Applications:
Percentage calculations are ubiquitous in various fields:
- Finance: Calculating interest rates, discounts, tax amounts, profit margins, and investment returns.
- Retail: Determining sale prices, markups, and discounts.
- Science: Expressing experimental results, error margins, and statistical data.
- Everyday life: Calculating tips, splitting bills, and understanding statistics in news reports.
Mastering Percentage Problems: Tips and Strategies
- Understand the keywords: Carefully read the problem statement to identify the known and unknown values. Words like "of," "is," and "what" are crucial indicators of the mathematical operations involved.
- Convert percentages to decimals or fractions: This simplifies the calculations and reduces the chance of errors.
- Choose the appropriate method: Select the method that you find most comfortable and efficient – algebraic approach, proportions, or decimal conversion.
- Check your work: Always verify your answer by substituting the solution back into the original problem.
- Practice regularly: The more you practice, the more confident and proficient you'll become in solving percentage problems.
Beyond the Basics: More Complex Scenarios
While the problem "20% of what number is 12?" provides a solid foundation, many real-world situations involve multiple percentage calculations or more complex scenarios. For instance:
- Compound interest: Interest is calculated not only on the principal amount but also on accumulated interest from previous periods.
- Successive discounts: Applying multiple discounts sequentially, where each discount is applied to the reduced price after the previous discount.
- Tax calculations involving multiple tax rates: Combining different tax rates to arrive at the final tax payable.
Addressing these complex situations requires a deeper understanding of percentage principles and potentially the use of more advanced mathematical techniques. However, mastering the fundamentals, as demonstrated in this article, will provide a strong base for tackling these more challenging problems.
In conclusion, solving "20% of what number is 12?" is not just about finding the answer (which is 60). It’s about understanding the underlying principles of percentages, exploring different solution methods, and building a solid foundation for tackling a wide range of percentage problems encountered in various aspects of life. The ability to confidently solve percentage problems is a valuable skill, applicable across numerous disciplines and crucial for effective decision-making in many aspects of life.
Latest Posts
Latest Posts
-
Is Sodium Acetate Soluble In Water
Apr 17, 2025
-
What Does The Suffix Ive Mean
Apr 17, 2025
-
80 Is What Percent Of 250
Apr 17, 2025
-
20 Is What Percent Of 36
Apr 17, 2025
-
What Is The Lcm Of 4 And 9
Apr 17, 2025
Related Post
Thank you for visiting our website which covers about 20 Percent Of What Number Is 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.