3 Out Of 40 As A Percentage
Kalali
Apr 08, 2025 · 5 min read
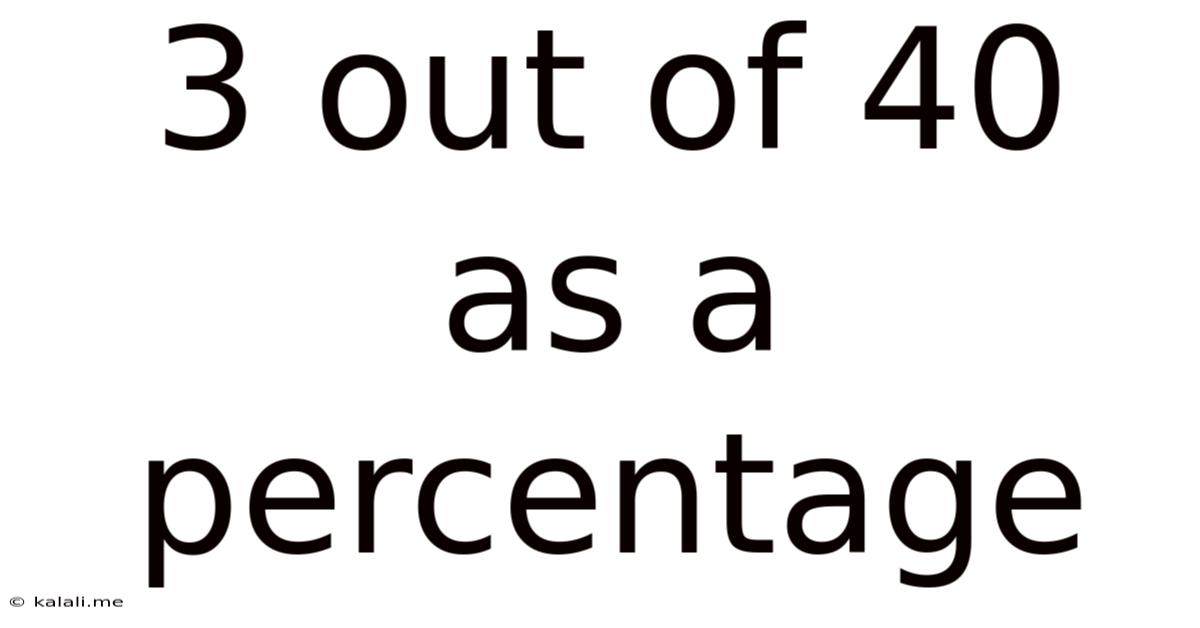
Table of Contents
3 Out of 40 as a Percentage: A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill applicable across numerous fields, from everyday budgeting to complex scientific analyses. Understanding how to convert fractions to percentages is crucial for interpreting data, making informed decisions, and excelling in various academic and professional settings. This comprehensive guide dives deep into calculating "3 out of 40 as a percentage," explaining the process step-by-step and exploring related concepts. We'll also cover different methods, practical applications, and troubleshooting common mistakes. This article will equip you with a thorough understanding of percentage calculations, allowing you to confidently tackle similar problems in the future.
What is a Percentage?
Before delving into the specific calculation, let's solidify our understanding of percentages. A percentage represents a fraction of 100. The word "percent" itself originates from the Latin "per centum," meaning "out of a hundred." Therefore, 50% means 50 out of 100, which is equivalent to the fraction ½ or the decimal 0.5. Percentages provide a standardized way to compare proportions and express parts of a whole.
Calculating 3 Out of 40 as a Percentage: The Step-by-Step Approach
The core principle of converting a fraction to a percentage involves transforming the fraction into an equivalent fraction with a denominator of 100. Let's break down the calculation of "3 out of 40 as a percentage":
-
Express the ratio as a fraction: "3 out of 40" is written as the fraction 3/40.
-
Convert the fraction to a decimal: Divide the numerator (3) by the denominator (40). 3 ÷ 40 = 0.075
-
Convert the decimal to a percentage: Multiply the decimal by 100%. 0.075 x 100% = 7.5%
Therefore, 3 out of 40 is equal to 7.5%.
Alternative Methods for Percentage Calculation
While the above method is straightforward, alternative approaches can be equally effective, especially with different calculators or when dealing with more complex fractions.
-
Using Proportions: Set up a proportion: 3/40 = x/100. Cross-multiply to solve for x: 40x = 300. Divide both sides by 40: x = 7.5. Therefore, x = 7.5%.
-
Using a Calculator with a Percentage Function: Many calculators have a dedicated percentage button (%). Simply enter 3 ÷ 40 = and then multiply the result by 100%.
-
Using Online Percentage Calculators: Numerous free online percentage calculators are readily available. Input the values (3 and 40), and the calculator will provide the result instantly. This is particularly useful for quick calculations or double-checking your manual work.
Practical Applications of Percentage Calculations
Understanding percentage calculations is vital in diverse real-world scenarios:
-
Academic Performance: Calculating grades, test scores, and overall academic progress often involves percentages. For example, if a student answers 3 out of 40 questions correctly on a test, their score is 7.5%.
-
Financial Management: Budgeting, calculating interest rates, understanding discounts, and analyzing investment returns all require working with percentages. A 7.5% discount on a product, for example, represents a significant saving.
-
Data Analysis: Percentages are used extensively in statistics and data analysis to represent proportions, trends, and changes over time. Analyzing survey results or market research often involves calculating percentages.
-
Science and Engineering: In fields like chemistry, physics, and engineering, percentages are used to express concentrations, efficiencies, and errors.
-
Everyday Life: From calculating tips at restaurants to understanding sales tax, percentages are encountered constantly in our daily routines.
Common Mistakes to Avoid When Calculating Percentages
Even seemingly simple percentage calculations can lead to errors if not approached carefully. Here are some common pitfalls to watch out for:
-
Incorrect Fraction Setup: Ensure you accurately represent the ratio as a fraction. In our example, ensuring the correct fraction is 3/40 is crucial. Mixing up the numerator and denominator will lead to an incorrect answer.
-
Decimal Point Errors: When converting decimals to percentages, ensure the decimal point is moved correctly. Multiplying by 100% effectively moves the decimal point two places to the right.
-
Rounding Errors: When rounding decimals, be mindful of significant figures and the level of precision required. Rounding too aggressively can lead to inaccurate results.
-
Misinterpretation of the Problem: Carefully read and understand the question before attempting the calculation. Ensure you are calculating the correct percentage. For example, “3 out of 40” is different from “40 out of 3” which would result in a vastly different percentage.
-
Calculator Errors: Always double-check your calculations, especially when using a calculator. Simple keystrokes errors can lead to significant mistakes.
Expanding on Percentage Concepts: Related Calculations
Understanding percentages extends beyond basic conversions. Related concepts include:
-
Percentage Increase/Decrease: Calculating the percentage change between two values requires subtracting the initial value from the final value, dividing the result by the initial value, and then multiplying by 100%. This is frequently used when comparing sales figures, population growth, or stock market performance.
-
Percentage Points: It’s essential to differentiate between percentage points and percentages. A change from 10% to 17% is a 7 percentage point increase but a 70% increase in the actual percentage.
-
Finding the Original Value: If you know the percentage and the final value, you can calculate the original value using algebraic techniques. For instance, if a product costs $30 after a 10% discount, you can use an equation to work backwards and find the original price.
-
Compound Interest: Compound interest calculations involve percentages compounded over time, impacting areas like savings accounts and loan repayments.
Conclusion
Calculating "3 out of 40 as a percentage," while seemingly simple, serves as a gateway to understanding a broader range of percentage-related problems. Mastering these fundamental calculations is essential for success in various academic, professional, and everyday situations. By understanding the step-by-step process, exploring alternative methods, and avoiding common errors, you can confidently tackle percentage calculations and effectively interpret data in a variety of contexts. Remember to always double-check your work and utilize resources like online calculators when necessary to ensure accuracy and efficiency. With practice, percentage calculations will become second nature, empowering you to confidently analyze and interpret numerical information.
Latest Posts
Latest Posts
-
10 Ml Is Equal To How Many Oz
Apr 17, 2025
-
Why Was The Continental Drift Rejected
Apr 17, 2025
-
4 Out Of 6 As A Percentage
Apr 17, 2025
-
What Elements Have One Valence Electron
Apr 17, 2025
-
What Is 4 To The Power Of 0
Apr 17, 2025
Related Post
Thank you for visiting our website which covers about 3 Out Of 40 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.