4 Out Of 18 As A Percentage
Kalali
Apr 24, 2025 · 5 min read
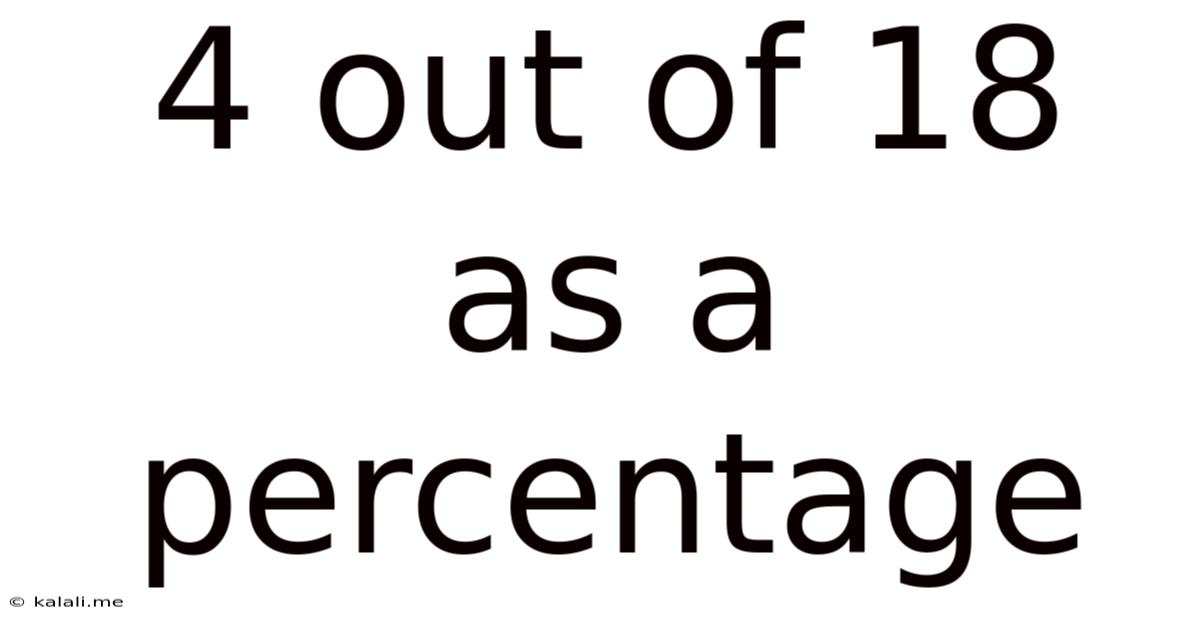
Table of Contents
4 out of 18 as a Percentage: A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill applicable across numerous fields, from finance and statistics to everyday life. Understanding how to convert fractions into percentages is crucial for interpreting data, making informed decisions, and communicating effectively. This article provides a comprehensive guide on calculating "4 out of 18 as a percentage," explaining the process step-by-step, exploring different methods, and offering practical applications. This will cover not only the basic calculation but also delve into related percentage concepts, helping you master this essential skill.
Meta Description: Learn how to calculate 4 out of 18 as a percentage. This comprehensive guide explains the process step-by-step, explores different methods, and provides practical examples to master percentage calculations.
Understanding the Basics of Percentages
Before diving into the calculation, let's establish a solid foundation. A percentage represents a fraction of 100. The word "percent" itself is derived from the Latin "per centum," meaning "out of one hundred." Therefore, any percentage can be expressed as a fraction with a denominator of 100. For example, 25% is equivalent to 25/100, which simplifies to 1/4.
This fundamental understanding is key to translating phrases like "4 out of 18" into a percentage. This phrase represents a fraction: 4/18. Our task is to convert this fraction into an equivalent fraction with a denominator of 100, thereby expressing it as a percentage.
Method 1: Converting the Fraction to a Decimal and then to a Percentage
This is arguably the most straightforward method. It involves two steps:
-
Convert the fraction to a decimal: Divide the numerator (4) by the denominator (18).
4 ÷ 18 ≈ 0.2222 (We'll round this to a manageable number of decimal places later)
-
Convert the decimal to a percentage: Multiply the decimal by 100.
0.2222 × 100 ≈ 22.22%
Therefore, 4 out of 18 is approximately 22.22%. The rounding introduces a slight inaccuracy, but for most practical purposes, this level of precision is sufficient.
Method 2: Simplifying the Fraction Before Conversion
This method enhances accuracy by simplifying the fraction before converting it to a decimal and then a percentage. Simplifying a fraction means reducing it to its lowest terms.
-
Simplify the fraction: Find the greatest common divisor (GCD) of the numerator and denominator. The GCD of 4 and 18 is 2. Divide both the numerator and the denominator by the GCD:
4 ÷ 2 = 2 18 ÷ 2 = 9
This simplifies the fraction to 2/9.
-
Convert the simplified fraction to a decimal: Divide the new numerator (2) by the new denominator (9).
2 ÷ 9 ≈ 0.2222
-
Convert the decimal to a percentage: Multiply the decimal by 100.
0.2222 × 100 ≈ 22.22%
This method yields the same result as Method 1, but the simplification step minimizes rounding errors, leading to a slightly more precise answer if you need greater accuracy.
Method 3: Using Proportions
This method is particularly helpful for understanding the underlying concept of percentages. We set up a proportion:
x/100 = 4/18
Here, 'x' represents the percentage we want to find. To solve for 'x', we cross-multiply:
18x = 400
Then, divide both sides by 18:
x = 400/18 ≈ 22.22%
This method demonstrates the equivalence between the fraction and the percentage, reinforcing the concept of "out of 100."
Rounding and Precision
As illustrated in the previous methods, rounding is often necessary when converting fractions to percentages. The level of precision required depends on the context. For informal calculations or general estimations, rounding to one or two decimal places (e.g., 22.2% or 22.22%) is usually sufficient. However, for scientific or financial applications, greater precision might be needed, requiring more decimal places or even using fractions instead of percentages.
Practical Applications of Percentage Calculations
The ability to calculate percentages has widespread practical applications:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns all rely heavily on percentage calculations. Understanding percentage changes is crucial for analyzing financial trends and making informed investment decisions. For example, calculating the percentage increase or decrease in your savings account balance over a period.
-
Statistics: Percentages are essential for representing and interpreting data. They are used to express probabilities, frequencies, and proportions within datasets. For instance, calculating the percentage of respondents who prefer a particular product in a market survey.
-
Everyday Life: Calculating tips in restaurants, understanding sale discounts, determining the percentage of a task completed, and interpreting nutritional information on food labels all involve percentage calculations. For example, determining the percentage of your daily caloric intake consumed from a particular meal.
-
Science: In scientific research, percentages are used to express concentrations, yields, and errors. For instance, calculating the percentage purity of a chemical compound or the percentage error in an experiment.
-
Education: Calculating grades and scores often involves percentages, providing a standardized way to assess student performance.
Beyond the Basic Calculation: Understanding Percentage Increase and Decrease
Understanding percentage change is a crucial extension of basic percentage calculations. This involves calculating the percentage increase or decrease between two values.
Percentage Increase: [(New Value - Old Value) / Old Value] x 100%
Percentage Decrease: [(Old Value - New Value) / Old Value] x 100%
Advanced Percentage Calculations: Compound Interest and Percentage Points
While this article focuses on the basic calculation of 4 out of 18 as a percentage, it's important to acknowledge more complex percentage applications:
-
Compound Interest: This involves calculating interest on both the principal amount and accumulated interest. The formula for compound interest is more complex than simple interest calculations and requires understanding exponential growth.
-
Percentage Points: It's crucial to distinguish between percentage points and percentage changes. A change of, say, 5 percentage points represents an absolute difference of 5%, while a 5% percentage increase signifies a relative change from a base value. For example, increasing from 10% to 15% is a 5 percentage point increase, but a 50% percentage increase.
Conclusion: Mastering Percentage Calculations
The ability to confidently calculate percentages is a vital skill with far-reaching applications. This article has provided a thorough explanation of how to calculate 4 out of 18 as a percentage, exploring various methods and emphasizing the importance of understanding the underlying principles. By mastering these techniques, you'll be well-equipped to handle percentage calculations in various contexts, from everyday situations to more complex mathematical and financial scenarios. Remember to always consider the level of precision required and choose the appropriate method accordingly. Further exploration of compound interest and other advanced concepts will solidify your understanding of this fundamental mathematical tool.
Latest Posts
Latest Posts
-
What Is 15 Percent Of 15
Apr 24, 2025
-
What Happens When Light Goes Through A Prism
Apr 24, 2025
-
What Is 4 Percent Of 40
Apr 24, 2025
-
How Big Is 90cm In Inches
Apr 24, 2025
-
What Is 10 Percent Of 160
Apr 24, 2025
Related Post
Thank you for visiting our website which covers about 4 Out Of 18 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.