40 Of 200 Is What Percent
Kalali
Apr 25, 2025 · 5 min read
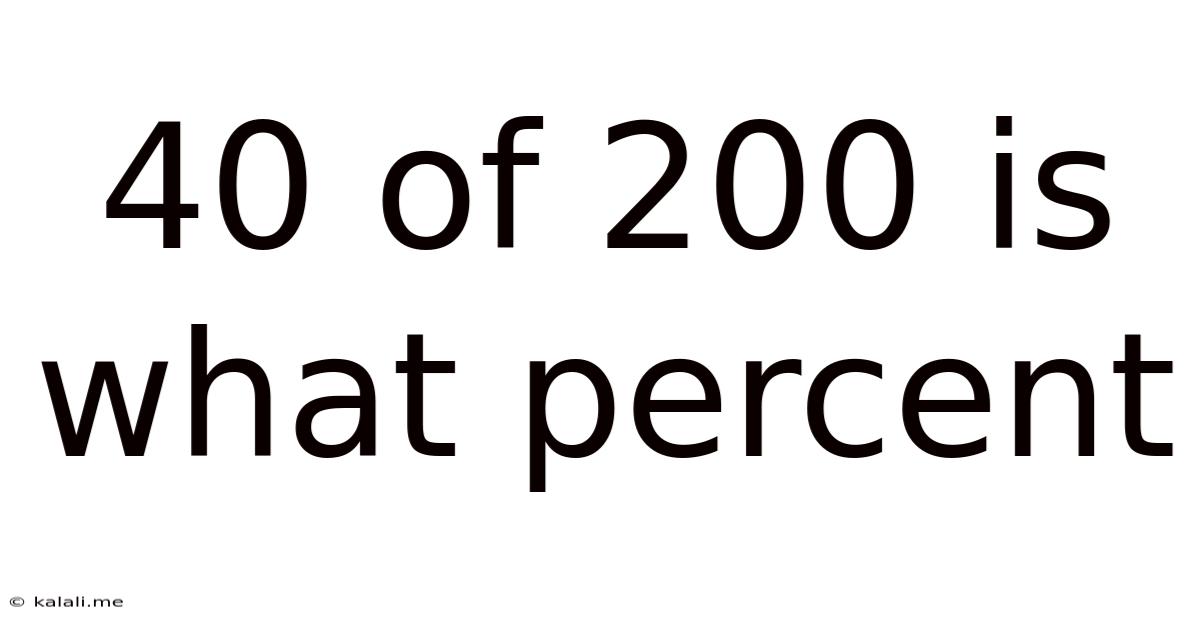
Table of Contents
40 out of 200 is What Percent? A Deep Dive into Percentage Calculations and Their Applications
Finding out what percentage 40 represents of 200 is a fundamental skill applicable across various fields, from everyday budgeting to complex statistical analysis. This article will not only answer the question directly but also explore the underlying concepts of percentages, different methods of calculation, and practical examples showcasing their real-world relevance. Understanding percentage calculations empowers you to interpret data, make informed decisions, and confidently tackle numerical challenges.
What is a Percentage?
A percentage is a way of expressing a number as a fraction of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of a hundred." Percentages are represented by the symbol "%". They provide a standardized way to compare proportions and make numerical relationships easier to understand. For example, instead of saying "3 out of 10," we can say "30%," immediately communicating the proportion more clearly.
Calculating 40 out of 200 as a Percentage: The Core Method
The most straightforward way to calculate the percentage is using the following formula:
(Part / Whole) * 100%
In this case:
- Part: 40
- Whole: 200
Therefore, the calculation is:
(40 / 200) * 100% = 20%
Therefore, 40 out of 200 is 20%.
Alternative Methods for Percentage Calculation
While the above method is the most common and generally preferred for its simplicity, there are alternative approaches that can be useful depending on the context and individual preference.
-
Using Decimals: We can convert the fraction 40/200 to a decimal by performing the division: 40 ÷ 200 = 0.2. Multiplying this decimal by 100% gives us 0.2 * 100% = 20%.
-
Simplifying the Fraction: Before performing the calculation, we can simplify the fraction 40/200 by dividing both the numerator and denominator by their greatest common divisor (GCD), which is 40. This simplifies the fraction to 1/5. Converting this to a percentage: (1/5) * 100% = 20%. This method is particularly helpful when dealing with larger numbers.
-
Cross-Multiplication: For those more comfortable with this technique, we can set up a proportion: 40/200 = x/100. Cross-multiplying gives us 200x = 4000. Solving for x, we get x = 20, so 40 out of 200 is 20%.
Practical Applications of Percentage Calculations
Understanding percentage calculations is crucial in many areas of life:
-
Finance: Calculating interest rates, discounts, tax rates, profit margins, and investment returns all rely heavily on percentage calculations. For instance, a 10% discount on a $100 item means a savings of $10.
-
Statistics: Percentages are essential for representing data in a clear and concise manner. They are used extensively in surveys, polls, and data analysis to show proportions and trends. Understanding percentage changes helps us track growth or decline in various metrics.
-
Science: Percentages are commonly used to express concentrations of solutions, experimental yields, and error margins in scientific experiments. For example, a 5% saline solution contains 5 grams of salt per 100 milliliters of solution.
-
Everyday Life: Percentage calculations are used in everyday situations such as calculating tips at restaurants, determining sale prices, understanding nutritional information on food labels, and interpreting statistics in news reports.
Advanced Percentage Calculations: Beyond the Basics
While calculating a simple percentage like 40 out of 200 is relatively straightforward, more complex scenarios often involve multiple steps or variations of the basic formula:
-
Percentage Increase/Decrease: Calculating the percentage increase or decrease between two numbers requires finding the difference between the two numbers, dividing this difference by the original number, and then multiplying by 100%. For example, if a price increases from $50 to $60, the percentage increase is (($60 - $50) / $50) * 100% = 20%.
-
Finding the Original Value: Sometimes you know the percentage and the resulting value, and you need to find the original value. For example, if a discounted item costs $80 after a 20% discount, the original price can be calculated by dividing $80 by (1 - 0.20) = $100.
-
Percentage Points: It's crucial to distinguish between percentage points and percentages. A change from 20% to 30% is a 10 percentage point increase, but it represents a 50% increase relative to the original 20%.
-
Compounding Percentages: When percentages are applied successively, such as compound interest, the calculations become more complex. The interest earned in one period becomes part of the principal for the next period, leading to exponential growth.
Troubleshooting Common Errors in Percentage Calculations
Several common mistakes can occur when working with percentages:
-
Incorrect Formula: Using the wrong formula or applying it incorrectly can lead to inaccurate results. Double-check your formula and the values you're using.
-
Decimal Errors: Inaccuracies in decimal calculations can significantly impact the final result. Pay attention to decimal points and round appropriately.
-
Confusing Percentage Points and Percentages: Remember the crucial distinction between percentage points and percentages to avoid misinterpretations.
-
Incorrect Interpretation: Even with accurate calculations, incorrect interpretation of the result can lead to flawed conclusions. Always consider the context and the meaning of the calculated percentage.
Conclusion: Mastering Percentages for a Data-Driven World
The ability to accurately calculate and interpret percentages is a valuable skill in today's data-driven world. While the core concept is relatively simple – expressing a number as a fraction of 100 – understanding different calculation methods, common applications, and potential pitfalls is crucial for effective problem-solving in various contexts. From managing personal finances to analyzing complex data sets, a solid grasp of percentage calculations empowers informed decision-making and enhances numerical literacy. By mastering these fundamental concepts, you equip yourself with a powerful tool for navigating the numerical aspects of life and work. Therefore, understanding that 40 out of 200 is 20% is just the beginning of a journey into the versatile world of percentages.
Latest Posts
Latest Posts
-
Is A Grasshopper A Primary Consumer
Apr 25, 2025
-
65 Out Of 75 As A Percentage
Apr 25, 2025
-
What Is 2 75 In A Fraction
Apr 25, 2025
-
What Percent Of 40 Is 3
Apr 25, 2025
-
What Does A Negative Slope Look Like
Apr 25, 2025
Related Post
Thank you for visiting our website which covers about 40 Of 200 Is What Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.