56 Out Of 60 As A Percentage
Kalali
Apr 16, 2025 · 5 min read
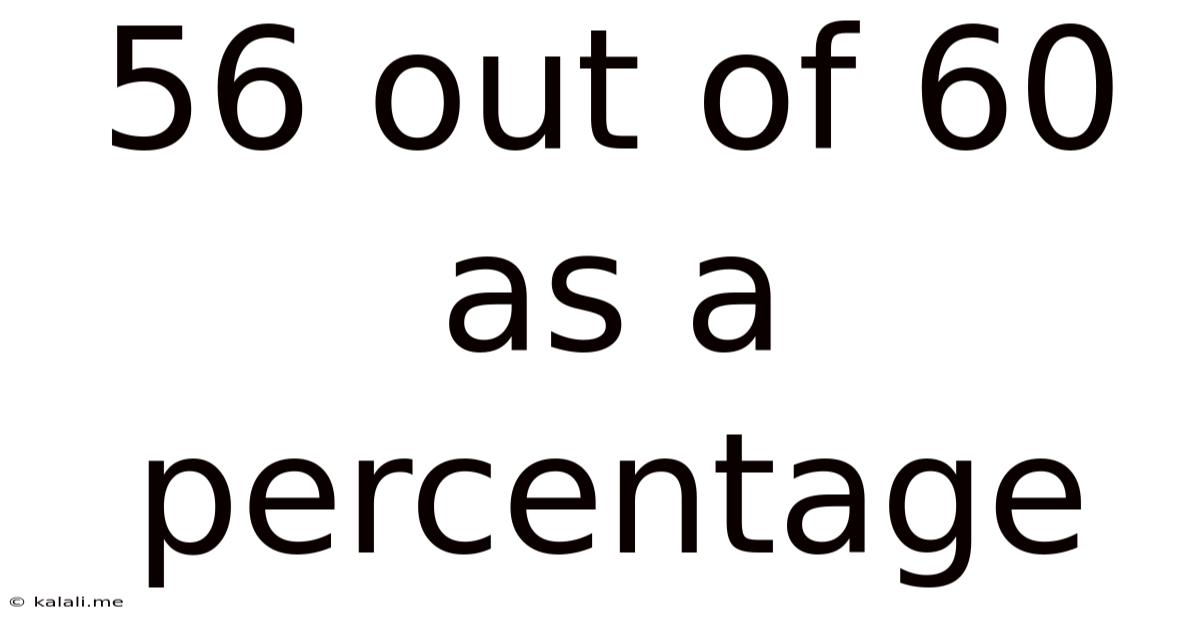
Table of Contents
56 out of 60 as a Percentage: A Comprehensive Guide to Percentage Calculations and Applications
Understanding percentages is a fundamental skill in various aspects of life, from academic assessments to financial transactions and everyday decision-making. This article will comprehensively explore how to calculate 56 out of 60 as a percentage, offering multiple approaches and delving into the broader applications of percentage calculations. We'll also cover common percentage-related problems and provide practical examples to solidify your understanding. This guide aims to be a definitive resource for anyone looking to master percentage calculations, regardless of their mathematical background.
Meta Description: Learn how to calculate 56 out of 60 as a percentage. This comprehensive guide covers multiple calculation methods, real-world applications, and explores common percentage-related problems. Master percentage calculations with this detailed tutorial.
Method 1: The Basic Percentage Formula
The most straightforward way to determine what percentage 56 represents out of 60 is using the basic percentage formula:
(Part / Whole) * 100% = Percentage
In this case:
- Part: 56 (the number we're interested in)
- Whole: 60 (the total number)
Therefore, the calculation is:
(56 / 60) * 100% = 93.333...%
Rounding to two decimal places, we get 93.33%. This means 56 represents 93.33% of 60.
Method 2: Using Decimal Equivalents
Another approach involves converting the fraction 56/60 into a decimal and then multiplying by 100%.
First, divide 56 by 60:
56 ÷ 60 = 0.93333...
Then, multiply the decimal by 100%:
0.93333... * 100% = 93.33% (rounded to two decimal places)
Method 3: Simplifying the Fraction
Before performing the calculation, we can simplify the fraction 56/60 by finding the greatest common divisor (GCD). The GCD of 56 and 60 is 4. Dividing both the numerator and the denominator by 4 simplifies the fraction to 14/15.
Now, we can calculate the percentage:
(14 / 15) * 100% ≈ 93.33%
Understanding the Result: 93.33%
The result, 93.33%, indicates that 56 is approximately 93.33% of 60. This percentage signifies a high proportion, suggesting a strong performance or a significant portion of a whole. The context in which this calculation is used will determine the interpretation of this percentage. For example, if this represents a test score, it suggests a very good performance. If it's a sales target, it signifies near-complete achievement.
Real-World Applications of Percentage Calculations
Percentage calculations are ubiquitous in various aspects of daily life. Here are some examples:
- Academic Performance: Calculating grades, class averages, and individual progress in school. For instance, a student scoring 56 out of 60 on a test achieved 93.33%.
- Financial Matters: Calculating interest rates, discounts, taxes, profit margins, and investment returns. Understanding percentages is crucial for making informed financial decisions. A 10% discount on a $100 item, for example, means a saving of $10.
- Statistics and Data Analysis: Percentages are used extensively in presenting and interpreting data, making complex information easily understandable. For example, analyzing survey results or market research often involves expressing data as percentages.
- Sales and Marketing: Calculating sales targets, conversion rates, market share, and customer acquisition costs. Businesses heavily rely on percentage calculations for performance monitoring and strategic planning.
- Everyday Life: Calculating tips in restaurants, determining sale prices in shops, and understanding nutritional information on food labels all involve using percentages.
Solving Related Percentage Problems
Let's explore some related problems to further solidify your understanding of percentage calculations:
Problem 1: Finding the Whole when the Percentage and Part are Known
If 56 represents 93.33% of a total number, what is the total number?
To solve this, we can rearrange the percentage formula:
Whole = (Part / Percentage) * 100
Whole = (56 / 93.33%) * 100 ≈ 60
Problem 2: Finding the Part when the Percentage and Whole are Known
What is 25% of 60?
We use the formula: Part = (Percentage / 100) * Whole
Part = (25 / 100) * 60 = 15
Problem 3: Finding the Percentage Increase or Decrease
If a value increases from 50 to 60, what is the percentage increase?
First, calculate the difference: 60 - 50 = 10
Then, divide the difference by the original value and multiply by 100%:
(10 / 50) * 100% = 20% increase
Advanced Percentage Concepts
Beyond basic calculations, understanding more advanced concepts can enhance your analytical skills:
- Compound Interest: This concept involves earning interest on both the principal amount and accumulated interest. Understanding compound interest is essential for long-term financial planning.
- Percentage Points: This represents the absolute difference between two percentages, not a relative change. For example, an increase from 10% to 20% is a 10 percentage point increase, not a 100% increase.
- Weighted Averages: This calculation assigns different weights to different values based on their importance. Weighted averages are used in various applications, including calculating GPA and portfolio performance.
Tips for Accurate Percentage Calculations
- Use a Calculator: For complex calculations or to ensure accuracy, use a calculator.
- Double-Check Your Work: Always double-check your calculations to avoid errors.
- Understand the Context: Pay close attention to the context of the problem to interpret the results accurately.
- Round Appropriately: Round your answers to an appropriate number of decimal places depending on the context. For instance, rounding to two decimal places is common for percentage calculations.
- Practice Regularly: The best way to master percentage calculations is through regular practice.
Conclusion
Calculating 56 out of 60 as a percentage, resulting in approximately 93.33%, is a simple yet crucial skill with wide-ranging applications. This article has explored various methods for calculating percentages, provided examples of real-world applications, and addressed common percentage-related problems. Mastering percentage calculations empowers you to make informed decisions in various aspects of your life, from academics and finance to daily tasks and professional endeavors. Remember to practice regularly and utilize the resources provided to build your confidence and proficiency in this fundamental mathematical skill. By understanding the underlying principles and applying the methods described, you can confidently tackle any percentage calculation you encounter.
Latest Posts
Latest Posts
-
Cuanto Es 27 Cm En Pulgadas
Apr 16, 2025
-
What Is 3 Oz In Ml
Apr 16, 2025
-
24 Is What Percent Of 20
Apr 16, 2025
-
Which Groups On The Periodic Table Contain Metalloids
Apr 16, 2025
-
What Percent Of 48 Is 36
Apr 16, 2025
Related Post
Thank you for visiting our website which covers about 56 Out Of 60 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.