9 4 As A Mixed Number
Kalali
Mar 30, 2025 · 5 min read
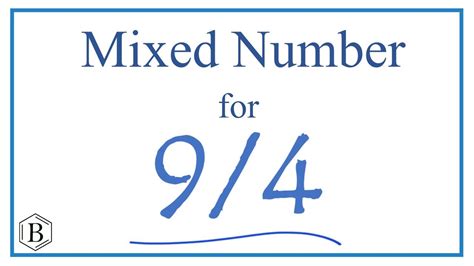
Table of Contents
9/4 as a Mixed Number: A Comprehensive Guide
Understanding fractions and how to convert them into mixed numbers is a fundamental skill in mathematics. This comprehensive guide will delve into the process of converting the improper fraction 9/4 into a mixed number, exploring the underlying concepts and providing practical examples to solidify your understanding. We'll also look at the broader context of improper fractions and mixed numbers, providing a solid foundation for future mathematical endeavors.
What is a Mixed Number?
A mixed number combines a whole number and a proper fraction. A proper fraction is a fraction where the numerator (the top number) is smaller than the denominator (the bottom number). For example, 1/2, 2/3, and 3/4 are all proper fractions. A mixed number represents a quantity that is greater than one. For instance, 1 1/2 represents one whole unit and one-half of another unit.
What is an Improper Fraction?
An improper fraction is a fraction where the numerator is greater than or equal to the denominator. Examples include 5/4, 7/2, and 9/4. Improper fractions represent a quantity greater than or equal to one. They are often easier to work with in calculations than mixed numbers, but mixed numbers are often preferred for representing quantities in real-world situations.
Converting 9/4 to a Mixed Number: The Process
The conversion of 9/4 to a mixed number involves determining how many whole units are contained within the fraction and expressing the remaining portion as a proper fraction. Here's a step-by-step guide:
-
Division: Divide the numerator (9) by the denominator (4).
9 ÷ 4 = 2 with a remainder of 1.
-
Whole Number: The quotient (2) represents the whole number part of the mixed number.
-
Proper Fraction: The remainder (1) becomes the numerator of the proper fraction, while the original denominator (4) remains the same. This gives us the proper fraction 1/4.
-
Mixed Number: Combine the whole number and the proper fraction to form the mixed number.
Therefore, 9/4 as a mixed number is 2 1/4.
Visual Representation: Understanding the Conversion
Imagine you have nine quarters (9/4). How many whole dollars can you make? You can make two whole dollars (2), and you'll have one quarter (1/4) left over. This visually represents the conversion of 9/4 to 2 1/4.
Why Convert Improper Fractions to Mixed Numbers?
Converting improper fractions to mixed numbers offers several advantages:
-
Clarity: Mixed numbers are often easier to understand and visualize than improper fractions, particularly in real-world applications. Saying "2 1/4 cups of flour" is clearer than "9/4 cups of flour".
-
Problem Solving: In some mathematical operations, particularly addition and subtraction, working with mixed numbers can be simpler and more intuitive than working with improper fractions.
-
Real-world Applications: Mixed numbers frequently appear in everyday situations, such as measuring ingredients in recipes, calculating distances, and representing quantities in various contexts.
Converting Mixed Numbers back to Improper Fractions
It's also important to understand the reverse process – converting a mixed number back into an improper fraction. This is useful for performing certain calculations. Let's take our example of 2 1/4:
-
Multiply: Multiply the whole number (2) by the denominator (4): 2 * 4 = 8
-
Add: Add the result to the numerator (1): 8 + 1 = 9
-
Improper Fraction: The resulting sum (9) becomes the numerator of the improper fraction, while the original denominator (4) remains the same.
Therefore, 2 1/4 converted back to an improper fraction is 9/4.
Further Exploration: Working with Improper Fractions and Mixed Numbers
Let's explore a few more examples to reinforce your understanding:
Example 1: Convert 11/3 to a mixed number.
- 11 ÷ 3 = 3 with a remainder of 2
- The whole number is 3.
- The proper fraction is 2/3.
- The mixed number is 3 2/3.
Example 2: Convert 17/5 to a mixed number.
- 17 ÷ 5 = 3 with a remainder of 2
- The whole number is 3.
- The proper fraction is 2/5.
- The mixed number is 3 2/5.
Example 3: Convert 25/8 to a mixed number.
- 25 ÷ 8 = 3 with a remainder of 1
- The whole number is 3.
- The proper fraction is 1/8.
- The mixed number is 3 1/8.
Example 4: Converting back to improper fractions
Let's convert 5 3/7 back to an improper fraction.
- Multiply the whole number by the denominator: 5 * 7 = 35
- Add the numerator: 35 + 3 = 38
- The improper fraction is 38/7
Practical Applications of Improper Fractions and Mixed Numbers
Improper fractions and their mixed number equivalents find practical application in numerous real-world scenarios:
-
Cooking and Baking: Recipes often call for fractional amounts of ingredients. Converting between improper fractions and mixed numbers helps in accurate measurement.
-
Construction and Engineering: Precise measurements are crucial in construction. Understanding and working with fractions ensures accuracy in building projects.
-
Finance and Accounting: Dealing with fractional shares of stocks or calculating interest often requires working with fractions.
-
Data Analysis: When dealing with statistical data, understanding fractions allows for accurate representation and interpretation of results.
Mastering Fractions: A Foundation for Mathematical Success
The ability to comfortably convert between improper fractions and mixed numbers is a key building block for more advanced mathematical concepts. Understanding these fundamental operations will pave the way for success in algebra, geometry, calculus, and other mathematical fields. Regular practice and a clear understanding of the underlying principles are crucial for mastery. Don't hesitate to work through numerous examples to solidify your understanding and build confidence in your abilities. The more you practice, the more natural and intuitive this process will become. Remember, consistent practice is the key to mastering any mathematical skill. Keep practicing, and you will soon become proficient in handling both improper fractions and mixed numbers with ease.
Latest Posts
Latest Posts
-
Cual Es El 10 Por Ciento De 1000
Apr 01, 2025
-
What Is 11 15 As A Percent
Apr 01, 2025
-
Un Triangulo Equilatero Es Tambien Un Triangulo
Apr 01, 2025
-
What Are The Inner Transition Metals
Apr 01, 2025
-
How Many Feet Is 1200 Meters
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about 9 4 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
