9 To The Power Of 5
Kalali
Apr 05, 2025 · 5 min read
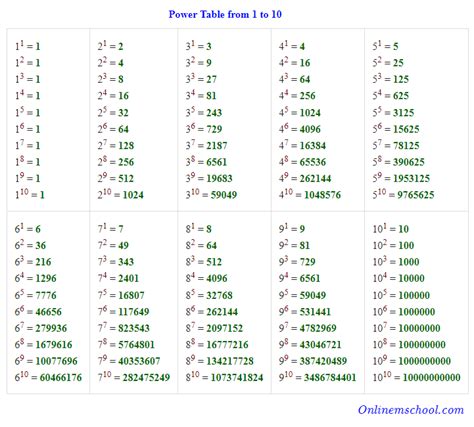
Table of Contents
9 to the Power of 5: Unveiling the Mathematical Marvel and its Applications
The seemingly simple expression "9 to the power of 5" (9⁵) hides a surprising depth, encompassing not just a straightforward mathematical calculation but also various applications across different fields. This article delves into the intricacies of this calculation, exploring its result, the underlying mathematical concepts, and its surprising relevance in areas ranging from computer science to finance.
Understanding Exponents and Powers
Before we dive into the specifics of 9⁵, let's establish a firm understanding of exponents. An exponent, also known as a power or index, indicates how many times a number (the base) is multiplied by itself. In the expression b<sup>n</sup>, 'b' represents the base and 'n' represents the exponent. Therefore, 9⁵ signifies 9 multiplied by itself five times: 9 x 9 x 9 x 9 x 9.
The Fundamental Concept: Repeated Multiplication
The concept of exponents simplifies the representation of repeated multiplication. Imagine trying to write out 9 multiplied by itself 100 times; the exponent notation makes this concise and manageable. This fundamental principle is crucial across numerous mathematical and computational tasks.
Expanding the Calculation: Step-by-Step Approach
Let's calculate 9⁵ step-by-step to illustrate the process:
- 9 x 9 = 81 (9 squared or 9²)
- 81 x 9 = 729 (9 cubed or 9³)
- 729 x 9 = 6561 (9 to the power of 4 or 9⁴)
- 6561 x 9 = 59049 (9 to the power of 5 or 9⁵)
Therefore, 9⁵ = 59049.
Beyond the Calculation: Exploring the Properties of Exponents
The calculation of 9⁵ is just one instance of applying the rules of exponents. Understanding these rules is crucial for more complex mathematical operations. Here are some key properties:
Product of Powers:
When multiplying two numbers with the same base, you add the exponents: b<sup>m</sup> * b<sup>n</sup> = b<sup>(m+n)</sup>. For example, 9² x 9³ = 9<sup>(2+3)</sup> = 9⁵.
Quotient of Powers:
When dividing two numbers with the same base, you subtract the exponents: b<sup>m</sup> / b<sup>n</sup> = b<sup>(m-n)</sup>. For example, 9⁵ / 9² = 9<sup>(5-2)</sup> = 9³.
Power of a Power:
When raising a power to another power, you multiply the exponents: (b<sup>m</sup>)<sup>n</sup> = b<sup>(mn)</sup>. For example, (9²)³ = 9<sup>(23)</sup> = 9⁶.
Power of a Product:
When raising a product to a power, you raise each factor to that power: (ab)<sup>n</sup> = a<sup>n</sup>b<sup>n</sup>. For example, (33)⁵ = 3⁵ * 3⁵ = 243 * 243 = 59049 (Note: 33 = 9, so this is equivalent to 9⁵).
Power of a Quotient:
Similarly, when raising a quotient to a power, you raise both the numerator and denominator to that power: (a/b)<sup>n</sup> = a<sup>n</sup>/b<sup>n</sup>.
Mastering these properties allows for efficient simplification and manipulation of exponential expressions, making complex calculations more manageable.
Applications of 9⁵ and Exponential Concepts
The seemingly abstract concept of raising a number to a power has widespread practical applications. Let's explore some key examples:
Computer Science and Data Storage:
Exponential growth is a fundamental concept in computer science. The capacity of data storage devices often increases exponentially. Understanding exponential growth is crucial for predicting future storage needs and developing efficient data management strategies. The number of possible combinations or permutations in cryptography also utilizes exponential calculations, impacting security systems significantly.
Financial Modeling: Compound Interest:
Compound interest, a cornerstone of finance, relies heavily on exponential functions. When interest is compounded, it's calculated not just on the principal but also on the accumulated interest from previous periods. This leads to exponential growth of investments over time. Calculating the future value of an investment with compound interest involves exponential equations.
Scientific Modeling and Growth Patterns:
Many natural phenomena exhibit exponential growth or decay. Population growth, radioactive decay, and the spread of infectious diseases often follow exponential patterns. Understanding exponential functions is crucial for modeling these phenomena and making predictions.
Probability and Combinatorics:
Exponential functions appear frequently in probability and combinatorics. Calculating the probability of certain events or the number of possible arrangements in a set often involves exponential calculations.
Engineering and Physics:
In various engineering and physics applications, exponential functions model decay or growth processes. For example, the decay of voltage in a circuit or the attenuation of a signal can be modeled using exponential functions.
Beyond 9⁵: Exploring Larger Powers and Advanced Concepts
While we've focused on 9⁵, the principles extend to much larger exponents. Calculating 9¹⁰⁰ or other high powers requires computational tools beyond manual calculations. The use of logarithms and calculators becomes essential for handling such magnitudes.
Furthermore, more advanced concepts like complex exponents and exponential functions build upon these fundamental principles. These advanced topics delve into the realm of calculus and have profound implications in fields like signal processing and quantum mechanics.
Conclusion: The Significance of 9⁵ and its Broader Context
The calculation of 9⁵, while seemingly straightforward, serves as a gateway to understanding a rich mathematical world. From the fundamental principles of exponents to their diverse applications across scientific and technological domains, the concept of raising a number to a power is both intellectually stimulating and practically relevant. The number 59049, the result of 9⁵, is not just a numerical answer; it represents the power of exponential functions and their pervasive influence in shaping our understanding of the world around us. The exploration of exponents opens doors to advanced mathematical concepts and expands our ability to model, predict, and solve problems in numerous fields. This journey beyond a simple calculation highlights the interconnectedness of mathematics and its vital role in our technological advancement and scientific progress.
Latest Posts
Latest Posts
-
Do You Need Insulation Wrapped Around Your Fractional Distillation Apparatus
Apr 06, 2025
-
Convert 120 Degrees Celsius To Fahrenheit
Apr 06, 2025
-
Venn Diagram Of Photosynthesis And Respiration
Apr 06, 2025
-
What Is The Lcm Of 2 And 3
Apr 06, 2025
-
10 To The Power Of 20
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about 9 To The Power Of 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
