Is Twenty Nine A Prime Number
Kalali
Mar 29, 2025 · 5 min read
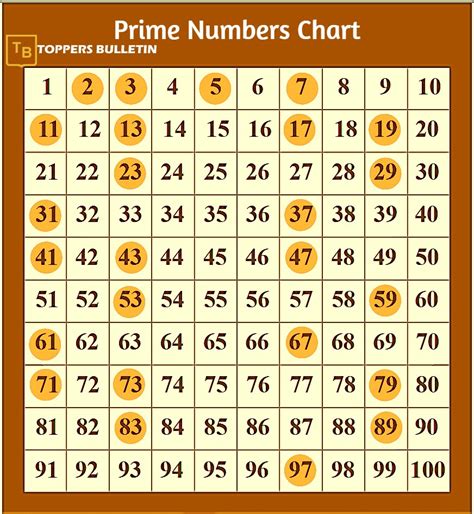
Table of Contents
Is Twenty-Nine a Prime Number? A Deep Dive into Prime Numbers and Divisibility
The question, "Is twenty-nine a prime number?" seems simple enough. However, exploring this seemingly straightforward question opens a fascinating door into the world of prime numbers, their properties, and their significance in mathematics. This article will not only definitively answer the question but delve into the concepts surrounding prime numbers, exploring various methods for determining primality and highlighting the importance of these fundamental building blocks of arithmetic.
Understanding Prime Numbers
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. This seemingly simple definition holds profound implications for number theory and cryptography. Prime numbers are the fundamental building blocks of all other integers, a concept solidified by the Fundamental Theorem of Arithmetic, which states that every integer greater than 1 can be uniquely represented as a product of prime numbers (ignoring the order of the factors). This unique factorization is crucial to many mathematical proofs and algorithms.
Let's consider some examples:
- 2: Divisible only by 1 and 2. Therefore, 2 is prime. It's also the only even prime number.
- 3: Divisible only by 1 and 3. Therefore, 3 is prime.
- 4: Divisible by 1, 2, and 4. Therefore, 4 is not prime (it's composite).
- 5: Divisible only by 1 and 5. Therefore, 5 is prime.
- 6: Divisible by 1, 2, 3, and 6. Therefore, 6 is not prime (it's composite).
Numbers that are not prime (and greater than 1) are called composite numbers. The number 1 is considered neither prime nor composite. This seemingly arbitrary exception is vital for the consistency of mathematical theorems and definitions.
Determining if a Number is Prime: Methods and Strategies
There are several ways to determine if a given number is prime. The simplest, though often inefficient for large numbers, is trial division. This involves checking for divisibility by all integers from 2 up to the square root of the number in question. If no integer within this range divides the number evenly, the number is prime.
Why the square root? If a number has a divisor greater than its square root, it must also have a divisor smaller than its square root. For instance, consider the number 100. Its divisors include 1, 2, 4, 5, 10, 20, 25, 50, and 100. Notice that 10 is the square root of 100. Divisors above 10 (20, 25, 50, 100) have corresponding divisors below 10 (5, 4, 2, 1).
Let's apply trial division to 29:
- Check for divisibility by 2: 29 is not divisible by 2 (it's odd).
- Check for divisibility by 3: 29 is not divisible by 3 (2 + 9 = 11, which is not divisible by 3).
- Check for divisibility by 5: 29 is not divisible by 5 (it doesn't end in 0 or 5).
- The square root of 29 is approximately 5.38. Therefore, we only need to check divisibility up to 5.
- Since 29 is not divisible by 2, 3, or 5, it is a prime number.
More Advanced Primality Tests
For larger numbers, trial division becomes computationally expensive. More sophisticated algorithms are employed, such as the Miller-Rabin primality test and the AKS primality test. These probabilistic tests offer a high degree of certainty about a number's primality without requiring exhaustive trial division. The AKS test is deterministic, guaranteeing a definitive answer, but it's less efficient than probabilistic methods for extremely large numbers.
The Significance of Prime Numbers
Prime numbers are far more than just a mathematical curiosity. Their significance extends to various fields:
- Cryptography: The security of many encryption algorithms, such as RSA, relies heavily on the difficulty of factoring large composite numbers into their prime factors. The larger the primes used, the more secure the encryption.
- Number Theory: Prime numbers form the bedrock of number theory, impacting countless theorems and proofs. Understanding their distribution and properties is a central focus of this branch of mathematics.
- Computer Science: Prime numbers play a role in hashing algorithms, random number generation, and other areas of computer science.
The Distribution of Prime Numbers
Prime numbers don't follow a readily predictable pattern. While there are infinitely many prime numbers (a fact proven by Euclid), their distribution is irregular. The Prime Number Theorem provides an approximation of the number of primes less than a given number, but it doesn't precisely pinpoint the location of each prime. The search for patterns in the distribution of primes remains an active area of mathematical research.
Answering the Question: Is Twenty-Nine a Prime Number?
Having explored the concept of prime numbers and methods for identifying them, we can definitively answer the initial question: Yes, twenty-nine is a prime number. As demonstrated through trial division, no integer other than 1 and 29 divides 29 evenly.
Beyond Twenty-Nine: Exploring Further
The journey into the world of prime numbers doesn't end with 29. Further exploration could involve:
- Finding larger prime numbers: The search for ever-larger prime numbers is an ongoing quest, with new record-breaking primes discovered regularly. These discoveries often involve significant computational resources and advanced algorithms.
- Exploring twin primes: Twin primes are pairs of prime numbers that differ by 2 (e.g., 3 and 5, 11 and 13). The twin prime conjecture, which postulates that there are infinitely many twin primes, remains unproven.
- Investigating prime gaps: Prime gaps refer to the differences between consecutive prime numbers. Understanding the distribution and behavior of prime gaps is another active area of research.
The seemingly simple question of whether 29 is prime has opened a door to a rich and complex field of mathematics. Prime numbers, with their seemingly random distribution yet fundamental importance, continue to fascinate and challenge mathematicians and computer scientists alike. Their role in securing our digital communications and underpinning fundamental mathematical principles underscores their profound significance in both theoretical and practical domains. The exploration of prime numbers is a journey of discovery, full of intriguing questions and ongoing research that pushes the boundaries of our mathematical understanding.
Latest Posts
Latest Posts
-
115 Out Of 125 As A Percentage
Apr 01, 2025
-
What Is 10 5 Inches In Cm
Apr 01, 2025
-
How To Find X And Y Intercepts In Vertex Form
Apr 01, 2025
-
What Is The Potential Difference Between The Plates
Apr 01, 2025
-
How Many Cups Are In 11 Oz
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Is Twenty Nine A Prime Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
