Lim Of Sinx X As X Approaches 0
Kalali
Jun 06, 2025 · 3 min read
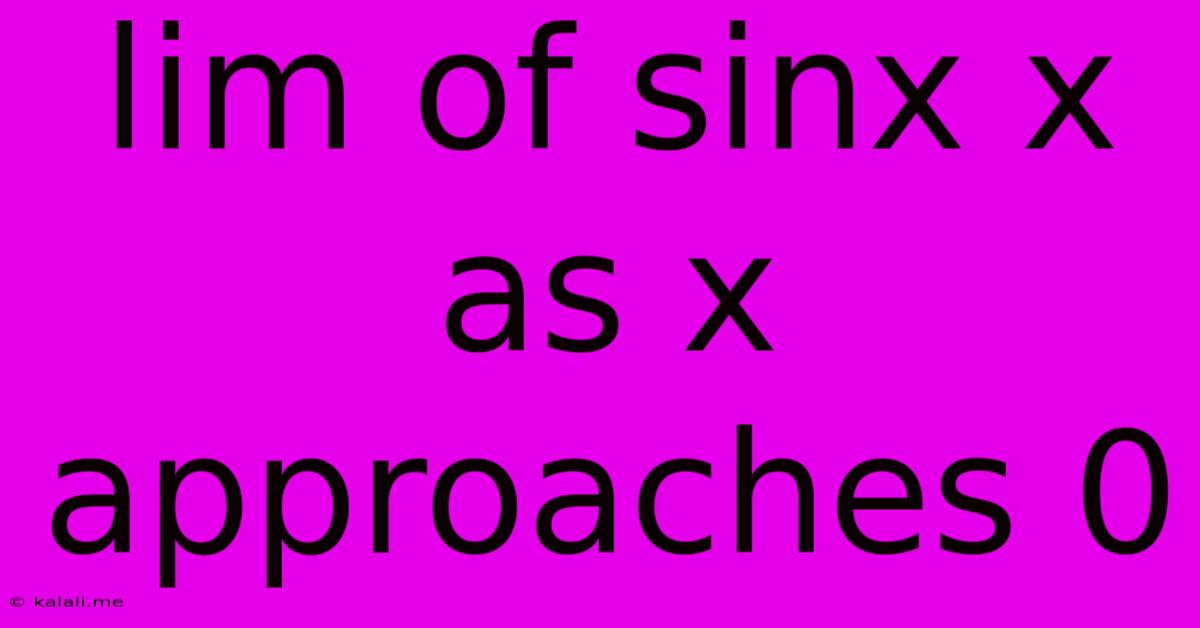
Table of Contents
Understanding the Limit of sin(x)/x as x Approaches 0
The limit of sin(x)/x as x approaches 0 is a fundamental concept in calculus and has significant applications in various fields of mathematics, physics, and engineering. This article will explore this limit, explaining its value, proof, and importance. Understanding this limit is crucial for mastering topics like derivatives, Taylor series, and Fourier analysis.
What is a Limit?
Before diving into the specifics, let's briefly revisit the concept of a limit. In simple terms, the limit of a function f(x) as x approaches a value 'a' (written as lim<sub>x→a</sub> f(x)) describes the value that f(x) approaches as x gets arbitrarily close to 'a', but not necessarily equal to 'a'. This is crucial because the function might not even be defined at x=a.
The Limit of sin(x)/x as x Approaches 0
The limit we're interested in is:
lim<sub>x→0</sub> sin(x)/x
Intuitively, you might try substituting x = 0 directly, but this results in an indeterminate form 0/0. This means we need a more sophisticated approach to evaluate this limit. The limit, however, surprisingly equals 1.
Proof using the Squeeze Theorem (Sandwich Theorem)
One of the most elegant ways to prove this limit is using the Squeeze Theorem. This theorem states that if we have three functions, f(x), g(x), and h(x), such that f(x) ≤ g(x) ≤ h(x) for all x in an interval around 'a' (except possibly at 'a' itself), and lim<sub>x→a</sub> f(x) = lim<sub>x→a</sub> h(x) = L, then lim<sub>x→a</sub> g(x) = L.
Consider a unit circle. Let x be the angle (in radians) subtended at the center by an arc of length x. Construct a triangle and sectors as shown in many calculus textbooks. By comparing the areas of these geometric figures, we can establish the following inequalities:
sin(x) ≤ x ≤ tan(x) for 0 < x < π/2
Dividing by sin(x) (since sin(x) > 0 for 0 < x < π/2), we get:
1 ≤ x/sin(x) ≤ 1/cos(x)
Taking the reciprocal (and reversing the inequality signs):
cos(x) ≤ sin(x)/x ≤ 1
As x approaches 0, cos(x) approaches 1. Therefore, by the Squeeze Theorem:
lim<sub>x→0</sub> sin(x)/x = 1
This proof holds for x approaching 0 from both the positive and negative sides.
Importance and Applications
This seemingly simple limit is fundamental in calculus and beyond:
- Derivatives: The derivative of sin(x) is proven using this limit.
- Taylor Series Expansion: The Taylor series expansion of sin(x) relies heavily on this limit.
- L'Hôpital's Rule: This limit is often encountered when applying L'Hôpital's Rule to solve indeterminate forms.
- Signal Processing: This limit is encountered in Fourier analysis, which is fundamental to signal processing.
- Physics and Engineering: Many physical phenomena are modeled using trigonometric functions, and this limit plays a vital role in their analysis.
Conclusion
The limit of sin(x)/x as x approaches 0 is a cornerstone of calculus and has far-reaching implications in various fields. Understanding its value (1) and its proof using the Squeeze Theorem is crucial for a solid grasp of many advanced mathematical concepts. Its significance extends well beyond the classroom, finding practical application in diverse areas of science and engineering.
Latest Posts
Latest Posts
-
How Long Does It Take For Thinset To Dry
Jun 06, 2025
-
Blender Texture Paint Not Working On Some Faces
Jun 06, 2025
-
Can You Create Clipping Masks With Pngs
Jun 06, 2025
-
How To Remove Moss From Brick
Jun 06, 2025
-
2007 Honda Shadow Aero Gas Tank Capacity In Litres
Jun 06, 2025
Related Post
Thank you for visiting our website which covers about Lim Of Sinx X As X Approaches 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.