What Is 5 Percent Of 180
Kalali
Apr 25, 2025 · 5 min read
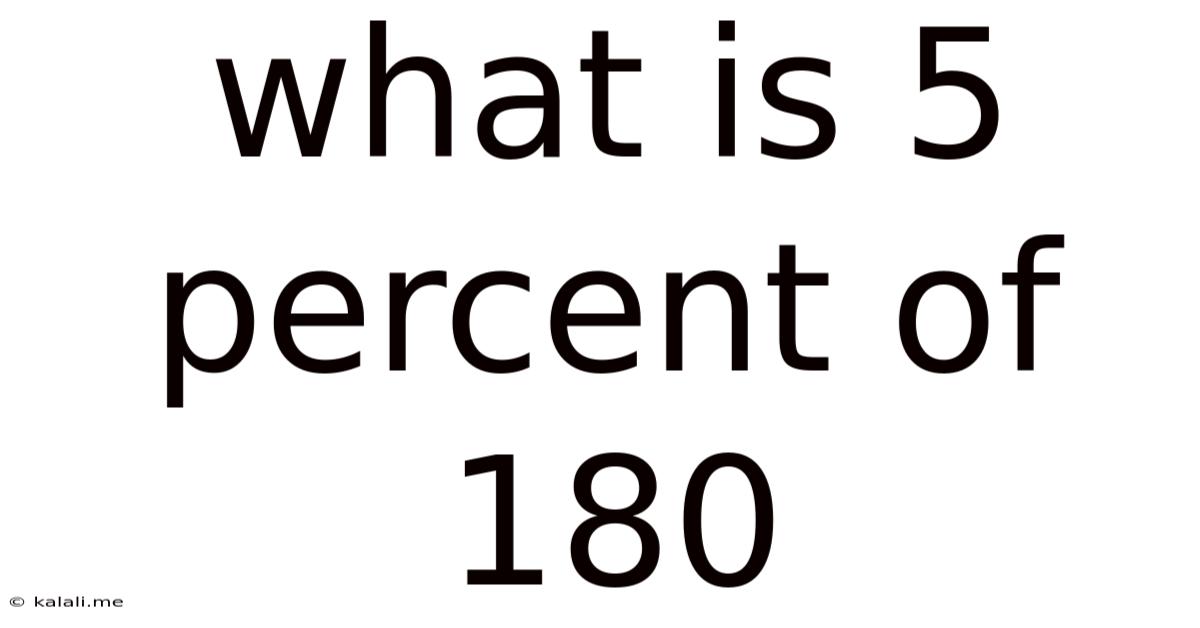
Table of Contents
What is 5 Percent of 180? A Deep Dive into Percentages and Their Applications
This seemingly simple question, "What is 5 percent of 180?", opens the door to a fascinating world of percentages, their practical applications, and the underlying mathematical principles. While the answer itself is easily calculable, understanding the how and why behind the calculation is crucial for navigating countless real-world scenarios, from calculating discounts and taxes to understanding financial reports and statistical data. This article will not only provide the answer but also explore the various methods for calculating percentages, their significance, and diverse applications across various fields.
Meta Description: Learn how to calculate 5 percent of 180 and understand the underlying mathematical principles. This comprehensive guide explores different methods, practical applications, and the importance of percentages in various fields.
Understanding Percentages: The Basics
Before diving into the calculation, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per hundred" or "out of 100". For example, 5% means 5 out of 100, which can be written as the fraction 5/100 or the decimal 0.05. This fundamental understanding is key to tackling any percentage problem.
Method 1: The Classic Formula
The most straightforward method to calculate 5 percent of 180 is using the basic percentage formula:
Percentage = (Part / Whole) x 100
However, in this case, we need to rearrange the formula to find the "part":
Part = (Percentage / 100) x Whole
Substituting our values:
Part = (5 / 100) x 180
Part = 0.05 x 180
Part = 9
Therefore, 5 percent of 180 is 9.
Method 2: Using Decimal Equivalents
This method leverages the decimal equivalent of a percentage. As mentioned earlier, 5% is equivalent to 0.05. Therefore, we can directly multiply 0.05 by 180:
0.05 x 180 = 9
This method is quick and efficient, especially for simple percentage calculations.
Method 3: Breaking it Down
For a deeper understanding, we can break down the calculation. If we want to find 5% of 180, we can first find 1% of 180 and then multiply by 5:
1% of 180 = 180 / 100 = 1.8
5% of 180 = 1.8 x 5 = 9
This method is particularly helpful when dealing with more complex percentages or when mental calculations are preferred.
Real-World Applications of Percentage Calculations
Understanding percentage calculations isn't just about solving mathematical problems; it's a crucial skill applicable across various domains:
-
Finance: Calculating interest rates, discounts, taxes (sales tax, VAT, GST), profit margins, returns on investment (ROI), and understanding financial statements all rely heavily on percentage calculations. For example, calculating a 5% discount on a $180 item is exactly the problem we just solved!
-
Retail: Stores frequently offer discounts like "20% off" or "buy one, get one 50% off". Understanding percentages is essential for consumers to make informed purchasing decisions and for retailers to set prices and manage sales.
-
Science and Statistics: Percentages are fundamental in representing data, expressing probabilities, and analyzing statistical trends. For example, expressing survey results, analyzing experimental outcomes, or understanding population demographics all involve percentage calculations.
-
Education: Grading systems often use percentages to represent student performance. Understanding percentages is vital for students to monitor their progress and for educators to assess student learning.
-
Everyday Life: From calculating tips at restaurants to understanding nutritional information on food labels, percentages are integrated into our daily routines.
Beyond the Basics: Advanced Percentage Calculations
While finding 5% of 180 is a simple calculation, the principles extend to more complex scenarios:
-
Calculating the Percentage Increase or Decrease: Imagine a price increases from $180 to $200. To find the percentage increase, we calculate the difference ($20), divide by the original amount ($180), and multiply by 100: (($20/$180) x 100) ≈ 11.11%.
-
Finding the Original Value: If an item is discounted by 5% and costs $171, we can work backward to find the original price. Let 'x' be the original price. Then, 0.95x = $171. Solving for x gives us x = $180.
-
Calculating Compound Interest: Compound interest involves earning interest on both the principal amount and accumulated interest. This requires more complex calculations involving exponential functions.
-
Percentage Change Over Time: Tracking changes in data over time, such as population growth, sales figures, or stock prices, often involves calculating percentage changes between different time periods.
Tools and Resources for Percentage Calculations
While manual calculations are essential for understanding the underlying principles, several tools can simplify the process:
-
Calculators: Most calculators have a percentage function, making calculations quick and easy.
-
Spreadsheets (like Excel or Google Sheets): Spreadsheets offer powerful functions for percentage calculations, allowing for complex analyses and data manipulation.
-
Online Percentage Calculators: Many websites offer free online calculators specifically designed for percentage calculations.
Conclusion: The Importance of Understanding Percentages
The seemingly simple question of "What is 5 percent of 180?" provides a springboard to understand the broader significance of percentages in various aspects of life. Mastering percentage calculations isn't just about solving mathematical problems; it's about developing a fundamental skill crucial for navigating financial decisions, interpreting data, and understanding the world around us. Whether you're a student, a professional, or simply someone who wants to improve their numerical literacy, a solid grasp of percentages is an invaluable asset. The ability to quickly and accurately calculate percentages empowers informed decision-making and enhances problem-solving capabilities in diverse situations. Remember, understanding the "why" behind the calculation is as important as getting the right answer.
Latest Posts
Latest Posts
-
Is A Grasshopper A Primary Consumer
Apr 25, 2025
-
65 Out Of 75 As A Percentage
Apr 25, 2025
-
What Is 2 75 In A Fraction
Apr 25, 2025
-
What Percent Of 40 Is 3
Apr 25, 2025
-
What Does A Negative Slope Look Like
Apr 25, 2025
Related Post
Thank you for visiting our website which covers about What Is 5 Percent Of 180 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.