What Is 6 Percent Of 20
Kalali
Apr 05, 2025 · 4 min read
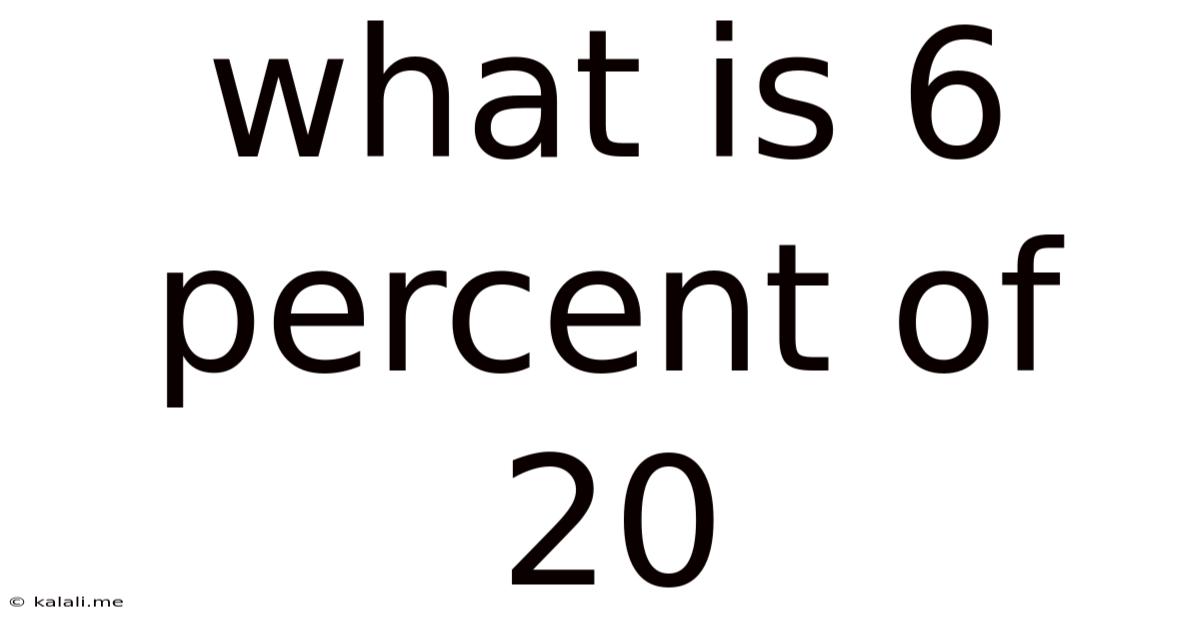
Table of Contents
What is 6 Percent of 20? A Deep Dive into Percentages and Their Applications
Finding 6 percent of 20 might seem like a simple calculation, but it opens the door to understanding a fundamental concept in mathematics and its widespread applications in various fields. This article will not only answer the question directly but will also explore the underlying principles of percentage calculations, different methods to solve the problem, and real-world examples illustrating the importance of percentages.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of a hundred." Therefore, 6 percent (6%) means 6 out of every 100. This fundamental understanding is crucial for grasping percentage calculations.
Key Concepts:
- The Whole: This is the total amount you're considering (in our case, 20).
- The Part: This is the portion of the whole you want to find (6% of 20).
- The Percentage: This is the rate expressed as a fraction of 100 (6%).
Calculating 6 Percent of 20: Three Methods
There are several methods to calculate 6% of 20. Let's explore three common approaches:
Method 1: Converting Percentage to Decimal
This is the most straightforward method. We convert the percentage to a decimal by dividing it by 100.
- Convert the percentage to a decimal: 6% ÷ 100 = 0.06
- Multiply the decimal by the whole: 0.06 x 20 = 1.2
Therefore, 6 percent of 20 is 1.2.
Method 2: Using Fractions
Percentages can also be expressed as fractions. 6% is equivalent to 6/100.
- Express the percentage as a fraction: 6% = 6/100
- Simplify the fraction (optional): 6/100 simplifies to 3/50
- Multiply the fraction by the whole: (3/50) x 20 = 60/50
- Simplify the resulting fraction: 60/50 = 6/5 = 1.2
Again, we arrive at the answer: 6 percent of 20 is 1.2.
Method 3: Using Proportion
This method uses the concept of ratios and proportions. We set up a proportion to solve for the unknown part.
- Set up a proportion: 6/100 = x/20 (where x is the unknown part)
- Cross-multiply: 6 x 20 = 100x
- Solve for x: 120 = 100x => x = 120/100 = 1.2
This method confirms that 6 percent of 20 is 1.2.
Real-World Applications of Percentage Calculations
Understanding percentages is essential in many real-world scenarios:
1. Finance and Investing:
- Interest Rates: Banks and financial institutions use percentages to calculate interest on loans and savings accounts. For example, a 6% interest rate on a $20,000 loan would result in a yearly interest payment of $1200.
- Investment Returns: Investors track their investment performance using percentages. A 6% return on a $20,000 investment would mean a profit of $1200.
- Taxes: Taxes are often expressed as percentages of income or the value of goods. Calculating tax amounts relies heavily on percentage calculations.
- Discounts: Sales and discounts are often advertised as percentages. A 6% discount on a $20 item would reduce the price by $1.20.
2. Science and Statistics:
- Data Analysis: Percentages are widely used in statistics to represent proportions and trends within datasets. For instance, researchers might find that 6% of a sample population exhibits a particular characteristic.
- Error Rates: In scientific experiments and measurements, error rates are often expressed as percentages to indicate the accuracy of the results.
- Probability: Probability, a core concept in statistics, often deals with percentages to represent the likelihood of certain events occurring.
3. Everyday Life:
- Tipping: People often tip service staff a certain percentage of the bill.
- Sales Tax: Sales tax is added to the price of goods and services, and is expressed as a percentage.
- Grading Systems: Many academic institutions use percentages to represent student grades.
Beyond the Basics: Advanced Percentage Calculations
While calculating 6% of 20 is a relatively simple task, understanding percentages extends to more complex scenarios. These might include:
- Calculating percentage increase or decrease: Determining the percentage change between two values. For example, if a value increases from 20 to 22, the percentage increase is calculated as [(22-20)/20] * 100% = 10%.
- Finding the original value: Given a percentage and the resulting value, finding the original value before the percentage change.
- Compounding percentages: Calculating the cumulative effect of repeated percentage changes over time, relevant for interest calculations and population growth.
- Working with multiple percentages: Calculating the combined effect of several percentage changes.
Conclusion: The Significance of Understanding Percentages
The seemingly simple calculation of 6% of 20 serves as a gateway to understanding the broader concept of percentages and their multifaceted applications. From financial planning and investment strategies to scientific research and everyday transactions, the ability to perform percentage calculations accurately and efficiently is a valuable skill with far-reaching implications. Mastering this fundamental mathematical concept enhances numerical literacy and improves decision-making across a wide range of fields. So, next time you encounter a percentage calculation, remember the simplicity and power of this fundamental tool. Understanding the ‘why’ behind the calculation, along with the various methods to achieve the answer, solidifies your understanding and empowers you to tackle more complex percentage problems with confidence.
Latest Posts
Latest Posts
-
2 Is What Percent Of 15
Apr 05, 2025
-
What Is 92 Degrees Fahrenheit In Celsius
Apr 05, 2025
-
Cual Es El Valor Absoluto De 3
Apr 05, 2025
-
24 Of 60 Is What Percent
Apr 05, 2025
-
Finding The Area Of Composite Shapes
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about What Is 6 Percent Of 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
