What Is 8/24 As A Percent
Kalali
Apr 17, 2025 · 5 min read
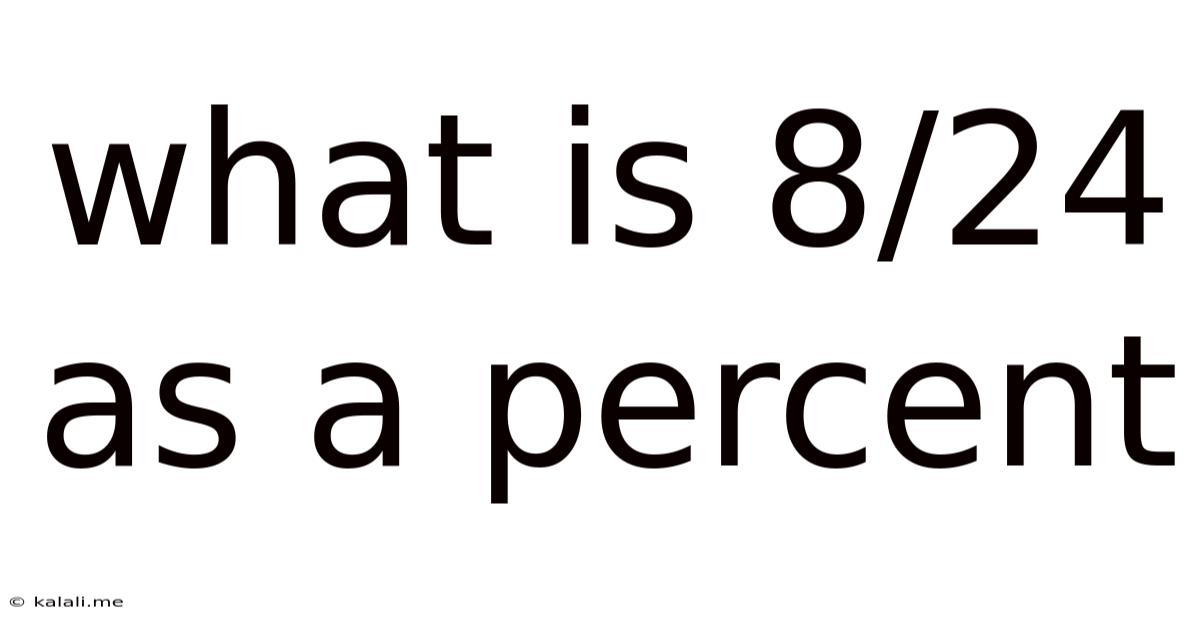
Table of Contents
What is 8/24 as a Percent? A Comprehensive Guide to Fraction-to-Percentage Conversion
This article will delve into the process of converting the fraction 8/24 into a percentage, exploring the underlying mathematical principles and offering practical applications. We'll cover various methods for solving this type of problem, providing a clear and comprehensive understanding for both beginners and those seeking a refresher. Understanding fraction-to-percentage conversion is crucial in various fields, from everyday calculations to complex financial analysis and scientific research. This guide aims to equip you with the skills and knowledge to confidently handle such conversions.
Meta Description: Learn how to convert the fraction 8/24 into a percentage. This comprehensive guide covers multiple methods, explains the underlying math, and provides practical applications of fraction-to-percentage conversions.
Understanding Fractions and Percentages
Before we dive into the conversion of 8/24, let's establish a firm understanding of fractions and percentages.
A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts you have, and the denominator indicates how many parts make up the whole. For example, in the fraction 8/24, 8 is the numerator and 24 is the denominator. This means we have 8 parts out of a total of 24 parts.
A percentage is a way of expressing a number as a fraction of 100. It uses the percent symbol (%) and indicates how many parts out of 100 are being considered. For instance, 50% means 50 parts out of 100, which is equivalent to one-half (1/2).
The key to converting a fraction to a percentage is understanding that percentages are essentially fractions with a denominator of 100.
Method 1: Simplifying the Fraction
The first step in converting 8/24 to a percentage is to simplify the fraction. Simplifying a fraction means reducing it to its lowest terms by dividing both the numerator and the denominator by their greatest common divisor (GCD).
The GCD of 8 and 24 is 8. Dividing both the numerator and denominator by 8 gives us:
8 ÷ 8 = 1 24 ÷ 8 = 3
Therefore, the simplified fraction is 1/3.
This simplification makes the subsequent conversion to a percentage much easier.
Method 2: Converting the Simplified Fraction to a Decimal
Now that we have the simplified fraction 1/3, we can convert it to a decimal by dividing the numerator (1) by the denominator (3):
1 ÷ 3 ≈ 0.3333...
The result is a repeating decimal, meaning the digit 3 repeats infinitely. For practical purposes, we can round this decimal to a suitable number of decimal places.
Method 3: Converting the Decimal to a Percentage
To convert the decimal 0.3333... to a percentage, we multiply it by 100 and add the percent symbol (%):
0.3333... × 100 ≈ 33.33%
Therefore, 8/24 is approximately equal to 33.33%. The use of "approximately" is crucial here because of the repeating decimal. In some contexts, rounding to a whole number (33%) might be sufficient, while others require more precision.
Method 4: Direct Conversion Using Proportions
Alternatively, we can convert the fraction to a percentage directly using proportions. We set up a proportion where the fraction 8/24 is equal to x/100, where x represents the percentage we want to find:
8/24 = x/100
To solve for x, we cross-multiply:
24x = 800
Now, divide both sides by 24:
x = 800 ÷ 24 ≈ 33.33
Therefore, x ≈ 33.33%, confirming our previous result.
Practical Applications of Fraction-to-Percentage Conversion
The ability to convert fractions to percentages has numerous practical applications across various fields:
-
Finance: Calculating interest rates, discounts, profit margins, and tax rates frequently involves converting fractions to percentages. For example, understanding that a 1/4 discount is equivalent to a 25% discount is essential for consumers and businesses alike.
-
Statistics: Representing data in percentages provides a clear and concise way to present proportions and probabilities. For example, if a survey shows that 8 out of 24 people prefer a particular product, the percentage (33.33%) offers a more readily understandable representation.
-
Science: In scientific experiments and research, many measurements and results are expressed as fractions, which are often converted to percentages for easier interpretation and comparison.
-
Everyday Life: Calculating tips, splitting bills, and understanding sale prices all involve working with fractions and percentages. For instance, calculating a 15% tip on a restaurant bill requires converting the percentage back into a fraction for calculation.
Understanding the Significance of Accuracy
The accuracy required when converting fractions to percentages depends heavily on the context. While rounding to 33% might suffice in casual situations, more precise calculations might demand retaining more decimal places (e.g., 33.33% or even 33.333%). Always consider the level of precision needed for the specific application. In scientific or financial contexts, maintaining high accuracy is paramount, while rounding is often acceptable for less critical scenarios.
Advanced Concepts: Recurring Decimals and Irrational Numbers
The conversion of 8/24 to a percentage introduces the concept of recurring decimals (33.33...). These decimals repeat infinitely. Understanding how to handle them, either by rounding or by representing them with a bar notation (0.3̅), is important. Some fraction conversions will yield irrational numbers, numbers that cannot be expressed as a simple fraction, such as π (pi). These require approximate values.
Conclusion: Mastering Fraction-to-Percentage Conversions
Converting fractions to percentages is a fundamental mathematical skill with broad applications. Mastering this skill involves understanding fractions, decimals, and the relationship between them. The process, while seemingly simple, requires attention to detail, especially when dealing with recurring decimals or the need for high accuracy. The methods outlined in this article provide a robust framework for converting fractions to percentages accurately and efficiently, regardless of the context. Remember to choose the appropriate level of precision based on your application's specific requirements. By understanding these concepts and practicing these methods, you'll confidently handle fraction-to-percentage conversions in various situations.
Latest Posts
Latest Posts
-
What Percentage Is 12 Out Of 14
Apr 19, 2025
-
What Is The Decimal For 9 20
Apr 19, 2025
-
2 Out Of 5 In Percentage
Apr 19, 2025
-
76 Is What Percent Of 80
Apr 19, 2025
-
How Many Hours Is 169 Minutes
Apr 19, 2025
Related Post
Thank you for visiting our website which covers about What Is 8/24 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.