What Is The Mean Of Sample Means
Kalali
Mar 28, 2025 · 6 min read
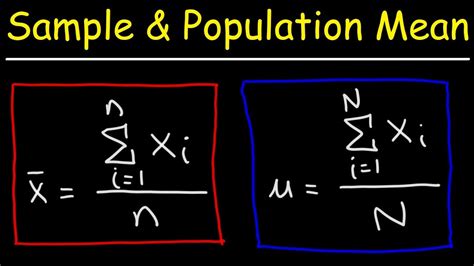
Table of Contents
What Does the Mean of Sample Means Really Mean? Understanding Sampling Distributions
The mean of sample means, also known as the expected value of the sample mean or the mean of the sampling distribution of the mean, is a fundamental concept in statistics. Understanding it is crucial for grasping inferential statistics, hypothesis testing, and confidence intervals. This article will delve deep into this concept, explaining its meaning, calculation, properties, and practical applications.
What is a Sampling Distribution?
Before we tackle the mean of sample means, we need to understand the concept of a sampling distribution. Imagine you have a large population – let's say, the heights of all adult women in a country. Measuring the height of every woman is impractical; instead, we take samples.
A sample is a smaller, representative subset of the population. If we repeatedly take samples of a fixed size (e.g., 100 women) and calculate the mean height for each sample, we won't get the same mean every time. These sample means will vary slightly.
The sampling distribution of the mean is the probability distribution of these sample means. It shows how the sample means are distributed across many different samples. It's not the distribution of the population itself, but rather the distribution of the means calculated from many samples of that population.
Calculating the Mean of Sample Means
The mean of sample means is the average of all the sample means obtained from repeated random sampling from a population. It's a key characteristic of the sampling distribution. Here's how it relates to the population mean:
The crucial point: Under certain conditions (discussed below), the mean of the sample means is equal to the population mean (μ). This is a powerful result that forms the basis of many statistical inferences.
Mathematically:
If we have 'k' samples, each with a mean (x̄₁, x̄₂, ..., x̄ₖ), then the mean of sample means (x̄) is:
x̄ = (x̄₁ + x̄₂ + ... + x̄ₖ) / k
As 'k' (the number of samples) approaches infinity, this mean of sample means converges to the population mean (μ).
The Central Limit Theorem: The Cornerstone of Understanding
The Central Limit Theorem (CLT) is the cornerstone of understanding the mean of sample means and its relationship to the population mean. It states that:
-
Regardless of the shape of the population distribution (as long as the population has a finite mean and variance), the sampling distribution of the mean will approximate a normal distribution as the sample size (n) increases.
-
The mean of this approximately normal sampling distribution will be equal to the population mean (μ).
-
The standard deviation of this sampling distribution, also known as the standard error of the mean (SEM), will be equal to the population standard deviation (σ) divided by the square root of the sample size (n): SEM = σ / √n.
The CLT is remarkable because it allows us to make inferences about the population mean even if we don't know the population distribution. This is hugely important in real-world applications where the true population distribution is often unknown.
Implications of the CLT
The CLT has profound implications:
-
Reduces reliance on population distribution: We can use the normal distribution to model the sampling distribution of the mean, regardless of the original population's shape. This simplifies statistical analysis significantly.
-
Improved accuracy with larger sample sizes: As the sample size increases, the sampling distribution becomes closer to a normal distribution, and the mean of sample means becomes a more precise estimate of the population mean. The standard error decreases as sample size increases, leading to more accurate inferences.
-
Basis for hypothesis testing and confidence intervals: The CLT is the foundation for constructing confidence intervals and performing hypothesis tests about the population mean. It allows us to determine the probability of observing a sample mean given a certain population mean.
Illustrative Example: Understanding the Concept Practically
Let's consider a simple example. Suppose we have a population of light bulbs with a mean lifespan (μ) of 1000 hours and a standard deviation (σ) of 100 hours. We don't know the exact shape of the population distribution, but we'll take multiple samples to understand the sample means.
-
Sampling: We take 100 random samples, each consisting of 25 light bulbs. For each sample, we calculate the mean lifespan.
-
Distribution of Sample Means: We'll plot the means of all 100 samples. According to the CLT, even if the population distribution of light bulb lifespans is not normal, the distribution of these sample means will be approximately normal, especially since we have a sample size of 25.
-
Mean of Sample Means: We then calculate the average of these 100 sample means. The CLT states that this average will be very close to the population mean (1000 hours).
-
Standard Error: The standard error of the mean (SEM) for our samples would be: SEM = 100 / √25 = 20 hours. This indicates that the sample means are likely to be within ±20 hours of the population mean.
Beyond the Mean: Other Aspects of the Sampling Distribution
While the mean of sample means is crucial, it's not the only important characteristic of the sampling distribution. Understanding the standard error of the mean (SEM) is equally vital. The SEM quantifies the variability of the sample means. A smaller SEM indicates that the sample means are clustered more tightly around the population mean, suggesting a more precise estimate.
The shape of the sampling distribution is also significant. The CLT guarantees an approximate normal distribution for large sample sizes, allowing us to use the properties of the normal distribution (like Z-scores and probabilities) for statistical inference.
Practical Applications: Where is This Used?
The mean of sample means and the CLT have widespread applications across various fields:
-
Quality Control: In manufacturing, sample means are used to monitor product quality. The mean of sample means helps determine if the production process is consistently meeting quality standards.
-
Market Research: Surveys often involve sampling a subset of the population. The mean of sample means from multiple surveys provides a more accurate estimate of population opinions or behaviors.
-
Medical Research: Clinical trials often rely on sample means to compare the effectiveness of different treatments. The CLT helps in determining statistically significant differences between treatment groups.
-
Environmental Science: Monitoring environmental parameters (e.g., pollution levels) typically involves sampling at different locations. The mean of sample means helps assess the overall average level of the parameter.
-
Finance: Stock prices and market returns are often analyzed using sampling techniques. The mean of sample means helps assess the average return of an investment.
Conclusion: Mastering the Mean of Sample Means for Statistical Inference
The mean of sample means, guided by the Central Limit Theorem, is a cornerstone of statistical inference. Understanding its properties and relationship to the population mean is critical for making valid conclusions from sample data. It allows us to use sample information to estimate population parameters with known levels of accuracy and confidence, bridging the gap between sample statistics and population parameters. Mastering this concept empowers us to make informed decisions based on data in a multitude of fields. The ability to interpret and apply the mean of sample means is a powerful tool in any statistician's arsenal.
Latest Posts
Latest Posts
-
What Is The Second Step In Dna Replication
Mar 31, 2025
-
220 C Is What In Fahrenheit
Mar 31, 2025
-
How Much Is 55 Cm In Inches
Mar 31, 2025
-
How Long It Takes To Boil Water
Mar 31, 2025
-
3 Of 20 Is What Percent
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about What Is The Mean Of Sample Means . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
