What Is The Percentage Of 2 8
Kalali
Apr 04, 2025 · 4 min read
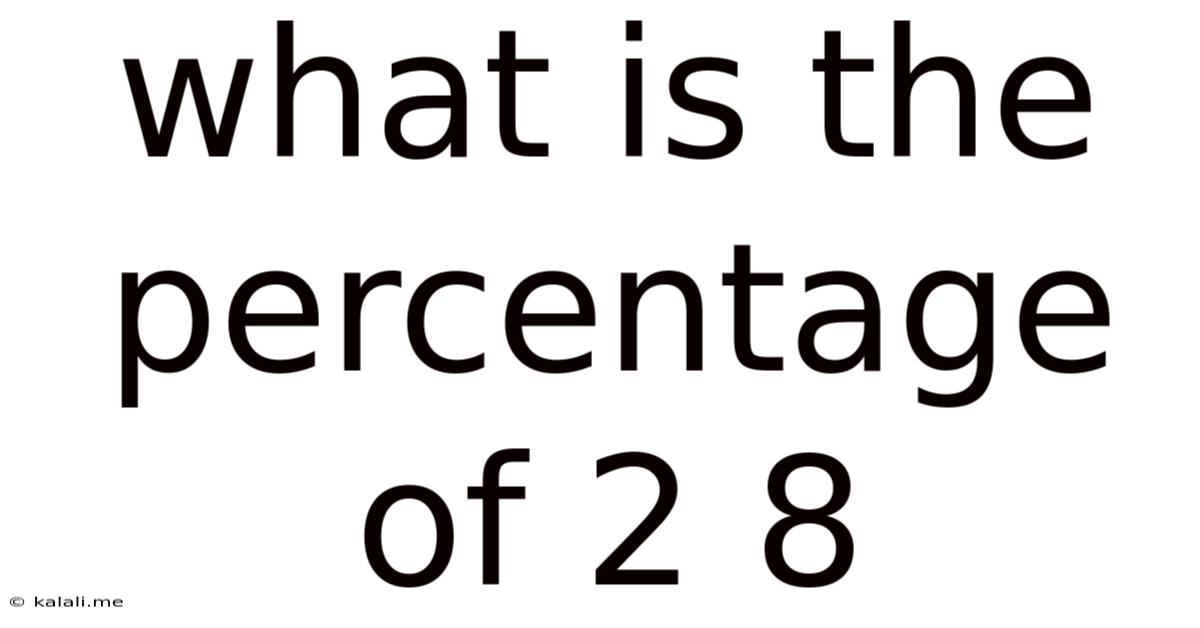
Table of Contents
- What Is The Percentage Of 2 8
- Table of Contents
- What is the Percentage of 2/8? A Comprehensive Guide to Fractions, Decimals, and Percentages
- Understanding Fractions
- Simplifying Fractions
- Converting Fractions to Decimals
- Converting Decimals to Percentages
- Different Methods for Calculating Percentages
- Method 1: Using Proportions
- Method 2: Using the Decimal Method (Alternative Approach)
- Method 3: Using a Calculator
- Real-World Applications of Percentage Calculations
- 1. Discounts and Sales
- 2. Taxes
- 3. Financial Calculations
- 4. Data Analysis and Statistics
- 5. Tip Calculations
- Beyond 2/8: Expanding Your Percentage Skills
- Latest Posts
- Latest Posts
- Related Post
What is the Percentage of 2/8? A Comprehensive Guide to Fractions, Decimals, and Percentages
Understanding percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts and tax to analyzing data and understanding statistics. This article will comprehensively explain how to determine the percentage represented by the fraction 2/8, covering the underlying concepts and offering practical examples to solidify your understanding.
Understanding Fractions
Before diving into percentages, let's solidify our grasp of fractions. A fraction represents a part of a whole. It consists of two numbers: a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into.
In our example, 2/8, the numerator is 2, and the denominator is 8. This means we have 2 parts out of a total of 8 equal parts.
Simplifying Fractions
Before converting a fraction to a percentage, it's often beneficial to simplify it. Simplifying a fraction means reducing it to its lowest terms by dividing both the numerator and the denominator by their greatest common divisor (GCD). The GCD of 2 and 8 is 2. Dividing both numbers by 2, we get:
2 ÷ 2 / 8 ÷ 2 = 1/4
This simplified fraction, 1/4, represents the same value as 2/8 but is easier to work with.
Converting Fractions to Decimals
To convert a fraction to a decimal, we divide the numerator by the denominator. In our simplified fraction, 1/4:
1 ÷ 4 = 0.25
Therefore, the decimal equivalent of 2/8 (or 1/4) is 0.25.
Converting Decimals to Percentages
The final step is converting the decimal to a percentage. To do this, we multiply the decimal by 100 and add the percentage symbol (%).
0.25 × 100 = 25%
Therefore, the percentage represented by the fraction 2/8 is 25%.
Different Methods for Calculating Percentages
While the above method provides a clear and straightforward approach, let's explore alternative methods to calculate percentages, offering flexibility depending on the context and your preferred calculation style.
Method 1: Using Proportions
We can express the problem as a proportion:
2/8 = x/100
Where 'x' represents the percentage we are trying to find. To solve for 'x', we cross-multiply:
8x = 200
x = 200/8
x = 25
Therefore, x = 25%, confirming our previous result. This method is particularly useful for mental calculations or when dealing with more complex fractions.
Method 2: Using the Decimal Method (Alternative Approach)
This method directly converts the fraction to a decimal and then to a percentage. We start with the fraction 2/8. First, we simplify:
2/8 = 1/4
Then, we convert the simplified fraction to a decimal:
1 ÷ 4 = 0.25
Finally, we convert the decimal to a percentage:
0.25 * 100% = 25%
Method 3: Using a Calculator
Modern calculators are equipped to handle fraction-to-percentage conversions efficiently. Simply enter the fraction (2/8) into your calculator and use the percentage function to obtain the result directly. This method is convenient and time-saving, particularly when dealing with more complex fractions or numerous calculations.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is crucial for navigating various aspects of daily life and professional endeavors. Here are some common applications:
1. Discounts and Sales
Retail stores frequently advertise discounts as percentages. For instance, a "25% off" sale means you'll pay 75% of the original price. Knowing how to calculate percentages allows you to quickly determine the final price after a discount.
2. Taxes
Sales tax, income tax, and other forms of taxation are often expressed as percentages. Understanding percentage calculations is essential for accurately determining the amount of tax owed and the total cost of a purchase including tax.
3. Financial Calculations
Percentages are fundamental in finance. Interest rates on loans and savings accounts are expressed as percentages, allowing you to calculate the interest earned or paid over time. Similarly, percentage changes in investments help track performance and assess risk.
4. Data Analysis and Statistics
Percentages are widely used in data analysis and statistics to represent proportions and trends. For example, survey results, election polls, and economic indicators often present data in terms of percentages to facilitate understanding and comparison.
5. Tip Calculations
Calculating tips in restaurants involves determining a percentage of the bill. Knowing how to calculate percentages ensures you can accurately tip according to your preference.
Beyond 2/8: Expanding Your Percentage Skills
While this article focused on calculating the percentage of 2/8, the principles discussed are applicable to any fraction. To calculate the percentage of any fraction, follow these steps:
- Simplify the fraction: Reduce the fraction to its lowest terms by finding the greatest common divisor of the numerator and denominator.
- Convert the fraction to a decimal: Divide the numerator by the denominator.
- Convert the decimal to a percentage: Multiply the decimal by 100 and add the percentage symbol (%).
Mastering percentage calculations is a valuable asset, empowering you to confidently tackle various mathematical challenges and real-world scenarios. Consistent practice and the application of these methods will build your skills and understanding. Remember to always double-check your work and utilize different methods to confirm your results and deepen your understanding of this fundamental mathematical concept.
Latest Posts
Latest Posts
-
75 Is What Percent Of 50
Apr 13, 2025
-
How Many Protons Are In Potassium
Apr 13, 2025
-
120 In Equals How Many Feet
Apr 13, 2025
-
How Many Ounces In 2000 Ml
Apr 13, 2025
-
A Continuous Random Variable May Assume What Value
Apr 13, 2025
Related Post
Thank you for visiting our website which covers about What Is The Percentage Of 2 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.