What Is The Smallest Multiple Of 3 And 4
Kalali
Apr 02, 2025 · 5 min read
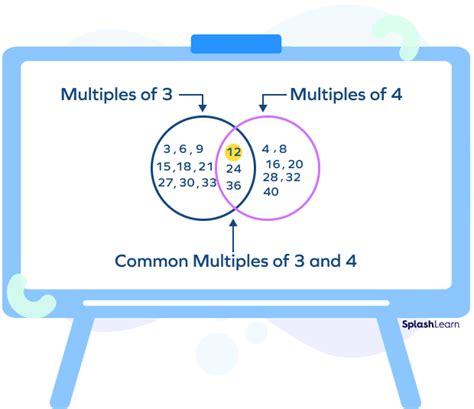
Table of Contents
What is the Smallest Multiple of 3 and 4? A Deep Dive into Least Common Multiples (LCM)
Finding the smallest multiple of 3 and 4 might seem like a simple arithmetic problem, solvable with a quick calculation. However, understanding the underlying mathematical principles involved—specifically, the concept of Least Common Multiples (LCM)—opens the door to tackling far more complex problems involving multiples of various numbers. This article will explore this seemingly simple question in detail, explaining the different methods to find the LCM, their applications, and extending the concept to more advanced scenarios.
Understanding Multiples
Before diving into the LCM, let's clarify what a multiple is. A multiple of a number is the product of that number and any integer (whole number). For example:
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30... and so on.
- Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40... and so on.
Notice that some numbers appear in both lists. These are the common multiples of 3 and 4. The question we're addressing is finding the smallest of these common multiples.
Finding the Least Common Multiple (LCM)
The Least Common Multiple (LCM) of two or more numbers is the smallest positive integer that is a multiple of all the numbers. There are several ways to find the LCM of 3 and 4:
Method 1: Listing Multiples
The most straightforward method is to list the multiples of each number until you find the smallest common one. As shown above:
- Multiples of 3: 3, 6, 9, 12, 15, 18...
- Multiples of 4: 4, 8, 12, 16, 20...
The smallest number appearing in both lists is 12. Therefore, the LCM of 3 and 4 is 12. This method works well for smaller numbers but becomes cumbersome for larger ones.
Method 2: Prime Factorization
A more efficient method, especially for larger numbers, uses prime factorization. This involves breaking down each number into its prime factors (numbers divisible only by 1 and themselves).
- Prime factorization of 3: 3 (3 is itself a prime number)
- Prime factorization of 4: 2 x 2 = 2²
To find the LCM using prime factorization:
- List the prime factors of each number.
- Identify the highest power of each prime factor present in the factorizations.
- Multiply these highest powers together.
In this case:
- Prime factors of 3: 3
- Prime factors of 4: 2²
- Highest powers: 2² and 3
- LCM = 2² x 3 = 4 x 3 = 12
This method is more efficient for larger numbers because it avoids lengthy lists of multiples.
Method 3: Using the Greatest Common Divisor (GCD)
The Greatest Common Divisor (GCD), also known as the Highest Common Factor (HCF), is the largest number that divides both numbers without leaving a remainder. The LCM and GCD are related by the following formula:
LCM(a, b) = (|a x b|) / GCD(a, b)
where 'a' and 'b' are the two numbers.
To find the LCM of 3 and 4 using this method:
- Find the GCD of 3 and 4: The only common divisor of 3 and 4 is 1. Therefore, GCD(3, 4) = 1.
- Apply the formula: LCM(3, 4) = (3 x 4) / 1 = 12
This method is particularly useful when dealing with larger numbers where finding the GCD is easier than directly finding the LCM. The Euclidean algorithm is a highly efficient method to calculate the GCD for larger numbers.
Applications of LCM
Understanding LCM isn't just about solving math problems; it has numerous real-world applications:
-
Scheduling: Imagine two buses arrive at a bus stop at different intervals. One bus arrives every 3 hours, and another every 4 hours. The LCM (12 hours) tells you when both buses will arrive simultaneously again.
-
Fraction addition and subtraction: Finding the LCM of the denominators is crucial for adding or subtracting fractions with unlike denominators. For example, to add 1/3 and 1/4, you'd find the LCM of 3 and 4 (12) and then rewrite the fractions with a common denominator of 12 before adding them.
-
Tiling and patterns: In design and construction, determining the size of tiles or the repetition of patterns often involves LCM. For instance, if you have tiles of size 3 units and 4 units, the LCM helps determine the smallest area that can be perfectly tiled without cutting the tiles.
-
Gear ratios: In mechanics, the LCM is useful in calculating gear ratios and determining when different gears will align.
-
Music: The LCM is applied in music theory to determine the least common multiple of the lengths of different notes or rhythmic patterns, helping to predict when musical phrases will coincide.
Extending the Concept: LCM of More Than Two Numbers
The methods described above can be extended to find the LCM of more than two numbers. Using prime factorization remains the most efficient approach.
For instance, to find the LCM of 3, 4, and 5:
- Prime factorization: 3 = 3, 4 = 2², 5 = 5
- Highest powers: 2², 3, 5
- LCM: 2² x 3 x 5 = 60
Similarly, the GCD method can also be extended to multiple numbers, though the calculation can become more complex.
Conclusion: The Power of Least Common Multiples
The seemingly simple question of finding the smallest multiple of 3 and 4 reveals a rich mathematical concept with far-reaching applications. Understanding the Least Common Multiple is a fundamental skill with practical relevance in various fields, from scheduling and construction to music and mechanics. While the listing method is intuitive for small numbers, the prime factorization method proves more efficient and versatile for larger numbers and more complex scenarios involving multiple numbers. Mastering the LCM not only strengthens your mathematical foundation but also equips you to solve practical problems across diverse domains. The ability to quickly and accurately calculate the LCM showcases a deeper understanding of number theory and its practical implications, making it a valuable skill in both academic and professional settings. Remember to practice these methods with different numbers to build your understanding and confidence in tackling LCM problems.
Latest Posts
Latest Posts
-
How Much Feet Is 66 Inches
Apr 03, 2025
-
How Do You Find The Mean On A Dot Plot
Apr 03, 2025
-
What Is 20 Percent Of 130
Apr 03, 2025
-
Equations With Variable On Both Sides
Apr 03, 2025
-
Do Lamprey Have Upright Erect Posture
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about What Is The Smallest Multiple Of 3 And 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
