What Percent Is 11 Out Of 20
Kalali
Apr 03, 2025 · 5 min read
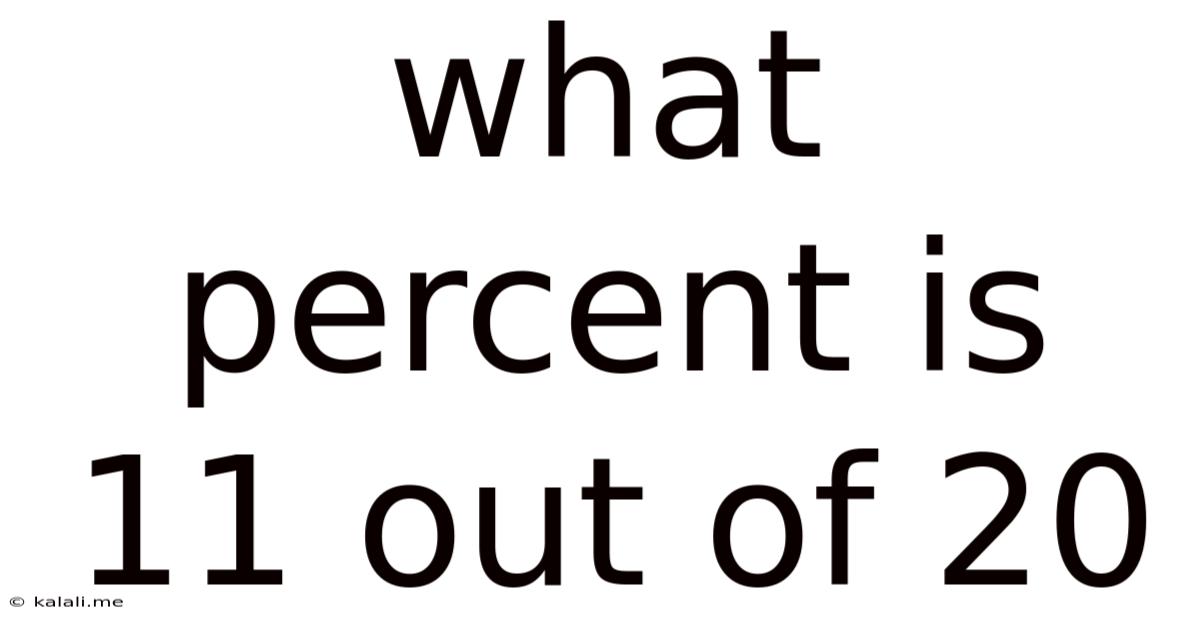
Table of Contents
What Percent is 11 Out of 20? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across numerous aspects of life, from calculating discounts and taxes to analyzing data and understanding statistics. This comprehensive guide delves into the question, "What percent is 11 out of 20?", providing not just the answer but a thorough explanation of the process, variations, and practical applications of percentage calculations.
Calculating the Percentage: 11 out of 20
The core of the problem lies in converting a fraction (11/20) into a percentage. A percentage represents a fraction of 100. To find the percentage, we follow these steps:
-
Express the fraction: We begin by expressing the given values as a fraction: 11/20. This means 11 represents a part of a whole, which is 20.
-
Convert the fraction to a decimal: To convert the fraction to a decimal, we divide the numerator (11) by the denominator (20): 11 ÷ 20 = 0.55
-
Convert the decimal to a percentage: To convert a decimal to a percentage, we multiply the decimal by 100 and add the percent symbol (%): 0.55 x 100 = 55%.
Therefore, 11 out of 20 is 55%.
Understanding the Concept of Percentages
Percentages are a convenient way to express proportions or ratios. They represent a fraction where the denominator is always 100. This standardized format makes comparisons and calculations easier. A percentage is essentially a way of expressing a part of a whole as a proportion of 100. For example:
- 50%: Represents 50 out of 100, or 1/2.
- 25%: Represents 25 out of 100, or 1/4.
- 10%: Represents 10 out of 100, or 1/10.
Understanding this basic principle is crucial for mastering percentage calculations.
Different Ways to Calculate Percentages
While the method described above is straightforward, there are alternative approaches to calculating percentages, depending on the given information and the context of the problem. Let's explore a few:
Method 1: Using Proportions
This method involves setting up a proportion to solve for the unknown percentage. The proportion would look like this:
x/100 = 11/20
To solve for 'x' (the percentage), we cross-multiply:
20x = 1100
Then, divide both sides by 20:
x = 55
Therefore, x = 55%, confirming our previous result.
Method 2: Using a Calculator
Most calculators have a percentage function. Simply enter 11 ÷ 20 and then multiply by 100 to get the percentage directly. This method is especially efficient for more complex calculations.
Method 3: Using Mental Math (for simpler calculations)
For simpler fractions, you can often estimate or calculate the percentage mentally. For example, knowing that 1/2 is 50%, you can easily deduce that 10/20 is 50%. Then, you can add the remaining 1/20 (which is 5%) to reach 55%. This method improves with practice and familiarity with common fractions and their percentage equivalents.
Practical Applications of Percentage Calculations
Percentage calculations are ubiquitous in various fields. Let's explore some examples:
1. Finance and Business:
- Calculating discounts: A store offers a 20% discount on an item priced at $100. The discount is 20% of $100, which is $20. The final price would be $80.
- Calculating taxes: A sales tax of 6% is applied to a purchase of $50. The tax amount is 6% of $50, which is $3. The total cost would be $53.
- Analyzing financial statements: Percentages are used to compare financial data over time or across different companies, allowing for better insights into financial performance. For instance, profit margins are expressed as a percentage of revenue.
- Calculating interest rates: Interest earned on savings accounts or paid on loans is usually expressed as a percentage.
2. Education:
- Calculating grades: A student's grade is often expressed as a percentage of the total possible points.
- Analyzing test scores: Percentages are used to compare student performance on tests and assessments.
3. Science and Statistics:
- Analyzing data: Percentages are used to represent proportions within datasets, enabling easier visualization and interpretation of trends.
- Calculating probabilities: Probability is often expressed as a percentage, indicating the likelihood of an event occurring.
4. Everyday Life:
- Calculating tips: Restaurant patrons typically leave a tip, often expressed as a percentage of the bill.
- Understanding sales: Sales are advertised as percentage reductions, allowing consumers to compare deals.
Beyond the Basics: Advanced Percentage Calculations
The principles discussed so far cover basic percentage calculations. However, more complex scenarios might require additional skills:
- Calculating percentage increase or decrease: This involves determining the percentage change between two values. The formula is:
((New Value - Old Value) / Old Value) x 100 - Calculating percentage points: Percentage points represent the difference between two percentages. For example, an increase from 10% to 15% is a 5 percentage point increase, not a 50% increase.
- Working with compound percentages: This involves calculating percentages on percentages, such as compound interest calculations.
Troubleshooting Common Errors in Percentage Calculations
Several common errors can occur when working with percentages:
- Confusing percentages and percentage points: Remember the distinction between these two concepts.
- Incorrectly calculating percentage change: Ensure you're using the correct formula for percentage increase or decrease.
- Misinterpreting the base: Clearly identify the base value (the whole) when calculating percentages.
Conclusion: Mastering the Power of Percentages
Understanding percentages is a valuable skill with wide-ranging applications. From the simple calculation of "what percent is 11 out of 20?" to more complex scenarios involving percentage change and compound interest, mastering this concept empowers you to navigate various situations more effectively. By practicing the methods outlined in this guide and understanding the underlying principles, you can confidently tackle percentage calculations in any context. Remember to always double-check your work and use a calculator when necessary to ensure accuracy. The ability to quickly and accurately calculate percentages is a valuable asset in numerous fields and everyday life.
Latest Posts
Latest Posts
-
4 9 As A Mixed Number
Apr 03, 2025
-
How Many Feet In 87 Inches
Apr 03, 2025
-
The Sex Pilus Is Found On The F Cell
Apr 03, 2025
-
How Many Acute Angles Does An Acute Triangle Have
Apr 03, 2025
-
How Is Density Related To The Layers Of The Earth
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is 11 Out Of 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
