What Percent Of 10 Is 3
Kalali
Apr 25, 2025 · 5 min read
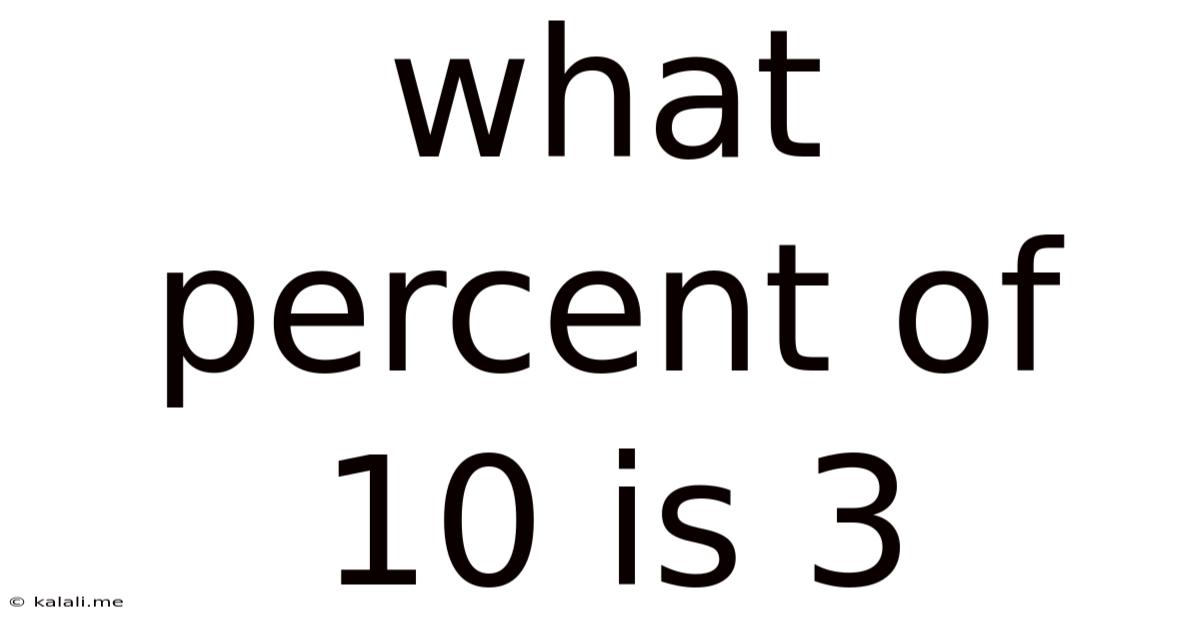
Table of Contents
What Percent of 10 is 3? A Deep Dive into Percentages and Their Applications
This seemingly simple question, "What percent of 10 is 3?", opens the door to a fascinating exploration of percentages, their mathematical underpinnings, and their widespread applications in everyday life. Understanding percentages is crucial for everything from calculating discounts and taxes to interpreting statistical data and making informed financial decisions. This article will not only answer the initial question but delve into the methods used to solve percentage problems, explore different approaches, and showcase real-world examples to solidify your understanding.
Meta Description: Learn how to calculate percentages, understand the concept of "what percent of 10 is 3," and explore real-world applications of percentage calculations in finance, statistics, and more. This comprehensive guide provides multiple solution methods and practical examples.
Understanding the Fundamentals of Percentages
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred" ( per centum in Latin). Therefore, 10% means 10 out of 100, which can be written as the fraction 10/100 or the decimal 0.10. Understanding this fundamental concept is key to solving percentage problems.
Solving "What Percent of 10 is 3?"
There are several methods to determine what percentage of 10 is 3. Let's explore three common approaches:
Method 1: Using Proportions
This method involves setting up a proportion, equating two ratios. We know that 3 is a part of 10, and we want to find the percentage, which is a fraction of 100. We can set up the proportion as follows:
3/10 = x/100
Where 'x' represents the unknown percentage. To solve for x, we cross-multiply:
10x = 300
Divide both sides by 10:
x = 30
Therefore, 3 is 30% of 10.
Method 2: Using Decimal Conversion
This method involves converting the fraction 3/10 into a decimal and then multiplying by 100 to express it as a percentage.
3/10 = 0.3
0.3 * 100 = 30%
This method is quick and efficient for simple percentage calculations.
Method 3: Using the Percentage Formula
The general formula for calculating percentages is:
(Part / Whole) * 100 = Percentage
In our case:
(3 / 10) * 100 = 30%
This formula provides a structured approach applicable to various percentage problems.
Expanding the Understanding: Variations on the Theme
Now that we've established that 3 is 30% of 10, let's explore some related questions and scenarios that build upon this fundamental understanding:
1. What is 30% of 100?
Using the percentage formula:
(30/100) * 100 = 30
This confirms that 30% of 100 is 30. This example highlights the direct relationship between percentages and their fractional equivalents.
2. What is 10% of 30?
Applying the formula:
(10/100) * 30 = 3
This illustrates the commutative nature of percentage calculations – the order doesn't affect the result.
3. If 3 is 30% of a number, what is the number?
Let's represent the unknown number as 'y'. We can set up the equation:
(3 / y) * 100 = 30
Solving for 'y':
300 = 30y
y = 10
This demonstrates how percentage calculations can be used to find the original whole amount when given a part and its percentage.
Real-World Applications of Percentage Calculations
The application of percentages extends far beyond simple mathematical exercises. Here are some examples of how percentages are used in real-life situations:
1. Finance and Budgeting:
- Interest rates: Banks and financial institutions use percentages to calculate interest on loans and savings accounts.
- Taxes: Sales tax, income tax, and property tax are all calculated as percentages.
- Discounts and markups: Stores use percentages to offer discounts on products or mark up prices for profit.
- Investment returns: Investors track their investment returns as percentages of their initial investment.
2. Statistics and Data Analysis:
- Data representation: Percentages are frequently used to represent data in charts and graphs, making it easier to visualize trends and patterns.
- Probability and chance: Percentages are used to express the likelihood of events occurring.
- Surveys and polls: Survey results are often presented as percentages to represent the proportion of respondents who chose specific options.
3. Everyday Life:
- Tipping in restaurants: People often calculate tips as a percentage of the bill amount.
- Calculating sales tax: Consumers need to understand sales tax percentages to determine the final price of goods and services.
- Understanding nutritional information: Food labels express nutritional values (like fat content) as percentages of recommended daily intakes.
Advanced Percentage Calculations and Considerations
While the basic percentage calculations are straightforward, more complex scenarios might require additional steps or considerations:
1. Compound Interest: This involves calculating interest on the principal amount plus accumulated interest from previous periods. Understanding compound interest is crucial for long-term financial planning.
2. Percentage Change: This is used to compare two values and determine the percentage increase or decrease between them. It's frequently used in financial reporting and economic analysis.
3. Percentage Points: It's important to distinguish between percentages and percentage points. A change from 10% to 20% is a 10 percentage point increase, but a 100% increase in the percentage itself.
Conclusion
The seemingly simple question, "What percent of 10 is 3?", serves as a gateway to understanding the multifaceted world of percentages. From calculating discounts to analyzing complex datasets, percentages are essential tools in numerous fields. Mastering percentage calculations empowers you to make informed decisions in various aspects of life, from managing personal finances to interpreting statistical data. This comprehensive guide offers multiple approaches to solve percentage problems and showcases their practical significance in the real world. Remember, consistent practice and a firm grasp of the underlying principles are key to mastering this fundamental mathematical concept.
Latest Posts
Latest Posts
-
What Is The Percentage Of 5 Out Of 15
Apr 25, 2025
-
What Is 60 Off Of 25
Apr 25, 2025
-
How Many Sides A Quadrilateral Have
Apr 25, 2025
-
Whats 3 To The Power Of 3
Apr 25, 2025
-
Least Common Multiple Of 9 And 5
Apr 25, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 10 Is 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.