What Percent Of 25 Is 4
Kalali
Apr 10, 2025 · 5 min read
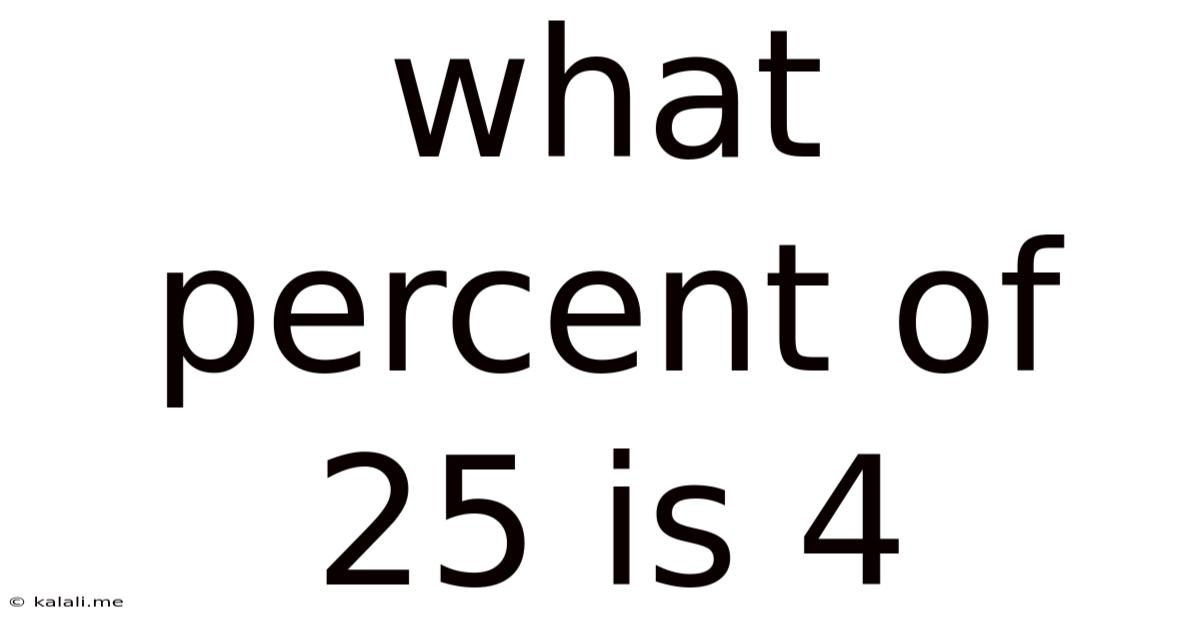
Table of Contents
What Percent of 25 is 4? A Deep Dive into Percentage Calculations and Their Applications
This seemingly simple question, "What percent of 25 is 4?", opens the door to a fascinating exploration of percentages, their practical applications, and the underlying mathematical principles. While the answer itself is easily calculated, understanding the why behind the calculation is crucial for navigating a world saturated with percentage-based data. This article will not only provide the solution but also delve into the various methods for solving percentage problems, exploring different approaches and their relevance in various contexts.
Meta Description: Learn how to calculate what percent of 25 is 4. This in-depth guide explains multiple methods, explores the underlying mathematics, and provides real-world examples showcasing the importance of percentage calculations in everyday life and various fields.
Understanding Percentages: The Basics
Before we tackle the specific problem, let's establish a solid understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The term "percent" literally means "per hundred." Therefore, 10% means 10 out of 100, which can be written as the fraction 10/100 or the decimal 0.10. This fundamental concept forms the basis for all percentage calculations.
Method 1: The Proportion Method
This classic approach uses the concept of proportions to solve percentage problems. We set up a proportion where one ratio represents the known values (4 out of 25) and the other ratio represents the unknown percentage (x out of 100). This is expressed as:
4/25 = x/100
To solve for x, we cross-multiply:
25x = 400
Then, we divide both sides by 25:
x = 16
Therefore, 4 is 16% of 25.
This method is particularly helpful for visualizing the relationship between the parts and the whole. It's a straightforward approach that's easily grasped by students learning about percentages. Furthermore, this method forms the basis for understanding more complex percentage calculations.
Method 2: The Decimal Method
This method leverages the decimal equivalent of a percentage. We first express the relationship between 4 and 25 as a fraction: 4/25. Then, we convert this fraction into a decimal by dividing the numerator (4) by the denominator (25):
4 ÷ 25 = 0.16
Finally, we convert the decimal to a percentage by multiplying by 100:
0.16 × 100 = 16%
This method is efficient and often preferred for its simplicity, especially when dealing with calculations that can be easily performed using a calculator. It's a direct and concise approach that avoids the need for cross-multiplication.
Method 3: The Formula Method
A more formulaic approach involves using the percentage formula directly:
Percentage = (Part / Whole) × 100
In our case, the part is 4, and the whole is 25. Substituting these values into the formula, we get:
Percentage = (4 / 25) × 100 = 0.16 × 100 = 16%
This method emphasizes the direct application of a formula, making it a useful technique for solving a wide range of percentage problems. It's systematic and easily adaptable to different scenarios.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is a vital skill applicable across numerous fields. Here are a few examples:
-
Finance: Calculating interest rates, discounts, profit margins, tax rates, and investment returns all rely heavily on percentage calculations. Understanding how percentages work is essential for making informed financial decisions. For example, determining the percentage increase or decrease in your savings account balance or understanding the annual percentage rate (APR) on a loan requires proficiency in percentage calculations.
-
Retail: Sales, discounts, and markups are expressed as percentages. Retailers use these calculations to attract customers, manage inventory, and determine profit margins. Understanding these calculations helps consumers make better purchasing decisions and compare prices effectively. For example, calculating the final price of an item after a 20% discount requires percentage calculation.
-
Science: Percentages are widely used in scientific research and data analysis to represent proportions, concentrations, and error margins. Statistical analysis often involves expressing results as percentages. For example, expressing the percentage of a particular element in a compound or the success rate of an experiment.
-
Education: Grades, test scores, and performance metrics in education are often represented as percentages. Students and educators use these to assess progress and identify areas for improvement. For example, understanding the percentage required to pass an exam or evaluating performance against a benchmark.
-
Everyday Life: From calculating tips at restaurants to understanding nutritional information on food labels, percentages are ubiquitous in our daily lives. Even figuring out the percentage of a task completed requires basic percentage calculations. For example, estimating the percentage of a project completed or determining what portion of a pie represents a certain percentage.
Beyond the Basics: More Complex Percentage Problems
While the problem "What percent of 25 is 4?" is relatively straightforward, understanding percentages extends far beyond these basic calculations. More complex problems involve:
-
Finding the whole when given the part and percentage: For instance, if 20% of a number is 10, what is the number?
-
Finding the part when given the whole and percentage: If 30% of a 500ml solution is acid, how many ml of acid are there?
-
Calculating percentage increase or decrease: Determining the percentage change between two values (e.g., comparing sales figures from year to year).
-
Compound percentages: This involves calculating percentages on top of previously calculated percentages, often seen in compound interest calculations.
Mastering these more complex aspects of percentage calculations will equip you to tackle a wider array of challenges in various fields. The fundamental principles remain the same, but the application and complexity increase. Practicing these more complex calculations will significantly enhance your understanding and proficiency.
Conclusion: The Importance of Percentage Literacy
The ability to accurately and efficiently calculate percentages is not just a mathematical skill but a crucial life skill. From navigating personal finances to understanding scientific data, percentages are fundamental to comprehending and interacting with the world around us. While the answer to "What percent of 25 is 4?" is a simple 16%, the journey of understanding the methods and applications behind this calculation provides a valuable insight into the power and practicality of percentages. This comprehensive understanding will empower you to approach percentage-related problems with confidence and efficiency, making you more capable of analyzing data and making informed decisions in various aspects of your life. Remember, practicing different methods and applying your knowledge to real-world examples is key to mastering percentage calculations.
Latest Posts
Latest Posts
-
2 To The Power Of 31
Apr 18, 2025
-
What Is 3 Out Of 20 As A Percentage
Apr 18, 2025
-
How Do You Know If A Table Is Linear
Apr 18, 2025
-
108 Is What Percent Of 200
Apr 18, 2025
-
How Much Is 50 Feet In Meters
Apr 18, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 25 Is 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.