What Percentage Is 10 Out Of 25
Kalali
Mar 28, 2025 · 5 min read
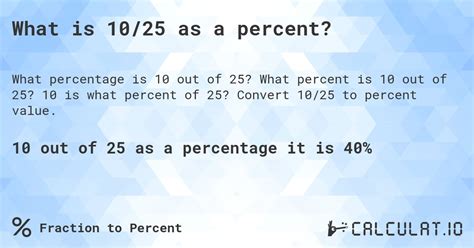
Table of Contents
What Percentage is 10 out of 25? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across numerous aspects of life, from calculating discounts and taxes to analyzing data and understanding financial reports. This comprehensive guide will not only answer the question "What percentage is 10 out of 25?" but also equip you with the knowledge and tools to confidently tackle similar percentage problems. We’ll explore different methods, delve into the underlying concepts, and provide practical examples to solidify your understanding.
Calculating the Percentage: The Basic Formula
The core of any percentage calculation lies in a simple formula:
(Part / Whole) * 100% = Percentage
In our specific case, "What percentage is 10 out of 25?", we can identify:
- Part: 10
- Whole: 25
Let's plug these values into the formula:
(10 / 25) * 100% = 40%
Therefore, 10 out of 25 is 40%.
Understanding the Concept: Parts of a Whole
Percentages represent fractions expressed as parts of a hundred. When we say 40%, we're essentially saying 40 out of 100. The calculation above shows how to convert a fraction (10/25) into its equivalent percentage (40/100). This conversion is crucial for understanding proportions and making comparisons.
Alternative Calculation Methods: Simplifying Fractions
Before applying the percentage formula, simplifying the fraction can make the calculation easier. We can simplify 10/25 by finding the greatest common divisor (GCD) of 10 and 25, which is 5. Dividing both the numerator and denominator by 5, we get:
10 ÷ 5 = 2 25 ÷ 5 = 5
This simplifies the fraction to 2/5. Now, applying the percentage formula:
(2 / 5) * 100% = 40%
This demonstrates that simplifying the fraction first can streamline the process, especially with larger numbers.
Visual Representation: Understanding Percentages Graphically
Visual aids can significantly improve understanding. Imagine a pie chart representing 25 equal slices. If 10 slices are shaded, this visually represents 10 out of 25, which, as we've calculated, is 40% of the whole pie. This visual approach can be especially helpful when dealing with larger datasets or explaining percentages to others.
Practical Applications: Real-World Examples of Percentage Calculations
Percentages are ubiquitous in everyday life. Here are a few examples illustrating their practical applications:
1. Sales and Discounts:
Imagine a store offering a 20% discount on a $50 item. To calculate the discount, we use the formula:
(20 / 100) * $50 = $10
The discount is $10, making the final price $40.
2. Tax Calculations:
Suppose a sales tax rate is 6%. To calculate the tax on a $100 purchase:
(6 / 100) * $100 = $6
The total cost, including tax, would be $106.
3. Grade Calculation:
A student scores 18 out of 20 on a test. What's their percentage score?
(18 / 20) * 100% = 90%
The student achieved a 90% score on the test.
4. Data Analysis:
In a survey of 500 people, 200 prefer Brand A. What percentage of respondents prefer Brand A?
(200 / 500) * 100% = 40%
40% of the survey respondents prefer Brand A.
5. Financial Investments:
If an investment grows from $1000 to $1200, the percentage increase is:
(($1200 - $1000) / $1000) * 100% = 20%
Advanced Percentage Calculations: Finding the Whole or the Part
The basic formula can be rearranged to solve for the whole or the part if other values are known:
Finding the Whole:
If you know the percentage and the part, you can find the whole using this formula:
Whole = (Part / Percentage) * 100
Example: If 20% of a number is 10, what is the number?
Whole = (10 / 20) * 100 = 50
Finding the Part:
If you know the percentage and the whole, you can find the part using this formula:
Part = (Percentage / 100) * Whole
Example: What is 30% of 200?
Part = (30 / 100) * 200 = 60
Percentage Increase and Decrease: Understanding Changes
Percentage increase or decrease calculations are common in various contexts, particularly in finance and economics.
Percentage Increase:
The formula is:
[(New Value - Original Value) / Original Value] * 100%
Example: A salary increases from $50,000 to $60,000. What's the percentage increase?
[(60000 - 50000) / 50000] * 100% = 20%
Percentage Decrease:
The formula is:
[(Original Value - New Value) / Original Value] * 100%
Example: The price of a product decreases from $100 to $80. What's the percentage decrease?
[(100 - 80) / 100] * 100% = 20%
Dealing with More Complex Scenarios: Multiple Percentages
Sometimes you need to work with multiple percentages in a single calculation. For example, calculating the final price after applying multiple discounts or taxes. In such cases, it's crucial to apply each percentage sequentially, not simply add them together.
Example: A product is discounted by 20%, then an additional 10% is applied. The initial price is $100.
- Step 1: 20% discount: (20/100) * $100 = $20 discount. Price becomes $80.
- Step 2: 10% discount on $80: (10/100) * $80 = $8 discount. Final price is $72.
Notice that the final discount isn't 30% but rather a slightly lower value due to the sequential application of discounts.
Mastering Percentages: Tips and Tricks for Success
- Practice regularly: The more you practice, the more confident you'll become.
- Use a calculator: For larger numbers or complex calculations, a calculator is essential for accuracy.
- Understand the concepts: Don't just memorize formulas; understand the underlying principles.
- Visualize the problem: Using diagrams or charts can help you grasp the concept better.
- Break down complex problems: Divide larger problems into smaller, manageable steps.
- Check your answers: Always double-check your calculations to ensure accuracy.
Conclusion: Unlocking the Power of Percentage Calculations
Understanding percentages is an invaluable skill that empowers you to analyze data, make informed decisions, and navigate various aspects of daily life with confidence. By mastering the basic formula and its variations, you'll be equipped to tackle a wide array of percentage problems, from simple calculations to more complex scenarios involving multiple percentages or finding unknown values. Remember to practice regularly and utilize visual aids to reinforce your understanding and build your proficiency in this essential mathematical skill. The seemingly simple question, "What percentage is 10 out of 25?" opens the door to a much broader understanding of percentages and their widespread applications.
Latest Posts
Latest Posts
-
What Percent Is 19 Out Of 25
Mar 31, 2025
-
What Type Of Ions Do Transition Metals Form
Mar 31, 2025
-
Chemical Change In Cooking An Egg
Mar 31, 2025
-
Is Grain Alcohol A Pure Substance Or Mixture
Mar 31, 2025
-
4 Right Angles And 2 Pairs Of Parallel Sides
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about What Percentage Is 10 Out Of 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
