What Percentage Is 15 Out Of 18
Kalali
Apr 22, 2025 · 6 min read
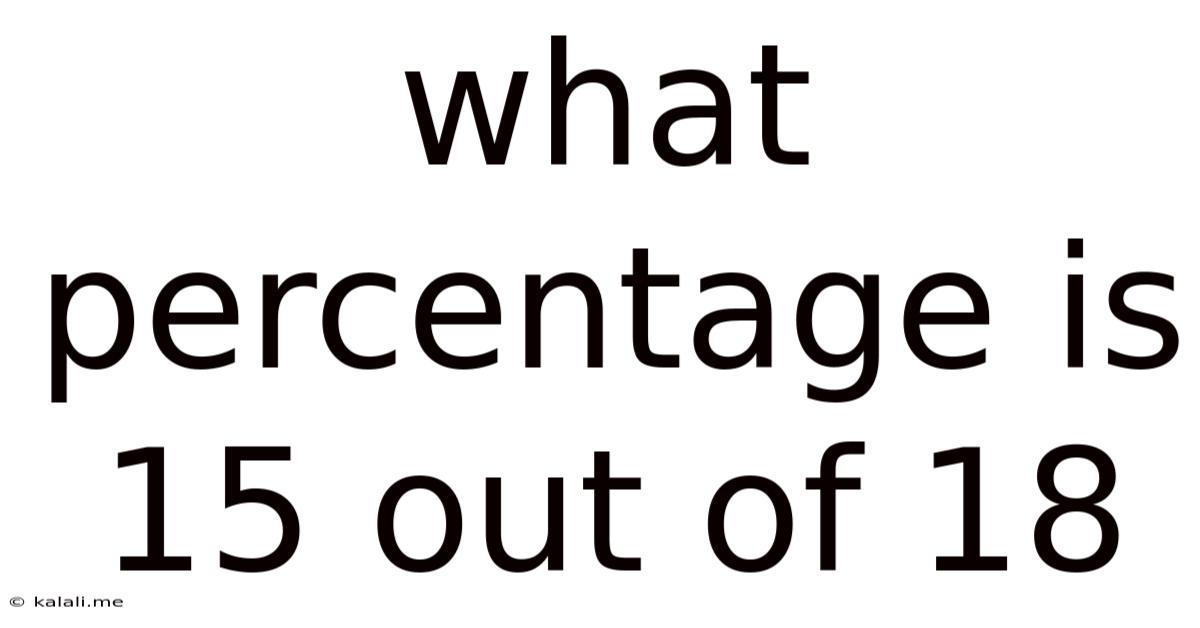
Table of Contents
What Percentage is 15 out of 18? A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill applicable across numerous fields, from everyday budgeting to complex financial analysis. Understanding how to determine what percentage 15 out of 18 represents is not only crucial for solving this specific problem but also builds a solid foundation for tackling similar percentage calculations. This comprehensive guide will not only provide the answer but also delve into the underlying methodology, exploring different calculation methods and providing practical examples to solidify your understanding. This will equip you to confidently calculate percentages in various scenarios.
Meta Description: Learn how to calculate percentages with a detailed explanation of determining what percentage 15 out of 18 represents. This guide covers different calculation methods and provides practical examples. Master percentage calculations for everyday use and beyond.
Understanding the Basics of Percentages
Before we dive into calculating the specific percentage, let's refresh our understanding of what percentages represent. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" signifies "per hundred." For instance, 50% means 50 out of 100, which is equivalent to ½ or 0.5.
Percentages are used to express proportions and make comparisons easier. They are widely used in various contexts, including:
- Finance: Interest rates, discounts, tax rates, profit margins
- Statistics: Data representation, probability calculations
- Science: Concentration measurements, experimental results
- Everyday Life: Sales, tips, grades
Method 1: Using the Formula (Classic Approach)
The most straightforward method to calculate the percentage is using the basic percentage formula:
(Part / Whole) * 100% = Percentage
In our case:
- Part: 15
- Whole: 18
Substituting these values into the formula:
(15 / 18) * 100% = 83.33% (approximately)
Therefore, 15 out of 18 is approximately 83.33%.
This method provides a clear and concise way to calculate the percentage, making it easily understandable for beginners. However, let's explore other methods for a more comprehensive understanding.
Method 2: Simplifying the Fraction
Before applying the percentage formula, we can simplify the fraction 15/18. Both 15 and 18 are divisible by 3:
15 ÷ 3 = 5 18 ÷ 3 = 6
This simplifies the fraction to 5/6. Now, we can apply the percentage formula:
(5 / 6) * 100% = 83.33% (approximately)
Simplifying the fraction beforehand can make the calculation easier, especially when dealing with larger numbers. It allows for more manageable numbers in the subsequent steps.
Method 3: Using Decimal Equivalents
Another approach involves converting the fraction into its decimal equivalent first, then multiplying by 100%:
15 ÷ 18 = 0.8333 (approximately)
0.8333 * 100% = 83.33% (approximately)
This method is particularly useful when using a calculator, as it streamlines the process. It avoids the need to directly multiply a fraction by 100%, simplifying the calculation.
Understanding the Significance of the Result: 83.33%
The result, 83.33%, indicates that 15 represents approximately 83.33% of 18. This percentage can be interpreted in various contexts. For example:
- Academic Performance: If a student answered 15 out of 18 questions correctly on a test, their score would be 83.33%.
- Sales Targets: If a salesperson aimed to make 18 sales and achieved 15, their performance would be 83.33% of the target.
- Project Completion: If a project comprised 18 tasks and 15 were completed, the project's completion rate would be 83.33%.
The precise meaning of this percentage depends heavily on the specific context in which it is used.
Handling Recurring Decimals: Precision and Rounding
Notice that the result, 83.33%, involves a recurring decimal (0.8333...). When dealing with recurring decimals in percentage calculations, it's essential to consider the required level of precision.
For most practical purposes, rounding to two decimal places (83.33%) is sufficient. However, in certain situations, greater precision might be necessary. For example, in financial calculations, rounding errors can accumulate and significantly impact the overall results. In such cases, retaining more decimal places or using fractions is advisable.
Advanced Applications and Related Concepts
The ability to calculate percentages extends beyond simple scenarios like "15 out of 18". It forms the basis of many more complex calculations, including:
- Percentage Increase/Decrease: Calculating the percentage change between two values. For instance, if a price increases from $10 to $15, the percentage increase is 50%.
- Percentage Points: A crucial concept in statistics, distinguishing between percentage change and percentage points. A change from 20% to 30% is a 10 percentage point increase, but a 50% increase in the percentage itself.
- Compound Interest: This involves calculating interest on both the principal amount and accumulated interest. Understanding percentages is fundamental to calculating compound interest.
- Proportional Reasoning: This broader mathematical concept relies heavily on understanding ratios and proportions, and percentages are a direct application of these principles.
Mastering percentage calculations isn't just about memorizing a formula; it's about grasping the underlying concepts and applying them flexibly to diverse situations.
Practical Examples: Real-World Applications
To solidify your understanding, let's look at some real-world examples where calculating percentages, similar to the 15 out of 18 scenario, becomes relevant:
Example 1: Sales Performance
A salesperson has a target of selling 24 products in a month. They managed to sell 21 products. What percentage of their target did they achieve?
(21 / 24) * 100% = 87.5%
The salesperson achieved 87.5% of their sales target.
Example 2: Exam Results
A student took an exam with 30 questions. They answered 24 correctly. What percentage of questions did they answer correctly?
(24 / 30) * 100% = 80%
The student answered 80% of the questions correctly.
Example 3: Discount Calculation
A store offers a 20% discount on an item originally priced at $50. What is the discounted price?
First, calculate the discount amount:
20% of $50 = (20/100) * $50 = $10
Then, subtract the discount from the original price:
$50 - $10 = $40
The discounted price is $40.
These examples highlight the versatility of percentage calculations across various fields. Understanding these calculations equips you to make informed decisions in numerous real-life situations.
Conclusion: Mastering Percentage Calculations
Calculating what percentage 15 represents out of 18 (approximately 83.33%) is a fundamental skill. This guide has explored various methods for calculating percentages, emphasizing the importance of understanding the underlying concepts. From the basic formula to simplifying fractions and using decimal equivalents, we've covered multiple approaches. Furthermore, we've delved into the practical applications of percentage calculations, highlighting their relevance in various fields and providing real-world examples. By understanding these concepts and practicing regularly, you'll gain confidence and proficiency in tackling percentage calculations, empowering you to analyze data, make informed decisions, and solve problems effectively in numerous situations. Remember, the key is not just the answer itself, but the understanding of the process and its broad applicability.
Latest Posts
Latest Posts
-
What Is 8 12 As A Percentage
Apr 22, 2025
-
2 Out Of 3 As A Percentage
Apr 22, 2025
-
How Many Liters In 64 Ounces
Apr 22, 2025
-
Cuanto Son 70 Grados Fahrenheit En Centigrados
Apr 22, 2025
-
Common Multiples Of 5 And 15
Apr 22, 2025
Related Post
Thank you for visiting our website which covers about What Percentage Is 15 Out Of 18 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.