What Percentage Is 4 Of 20
Kalali
Apr 17, 2025 · 5 min read
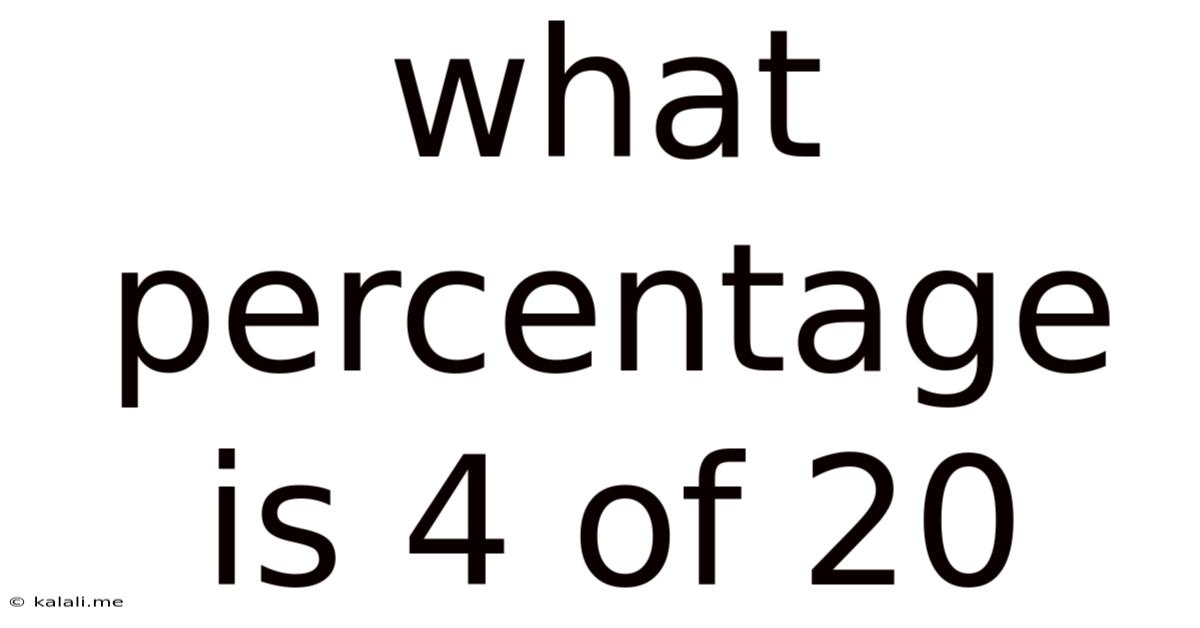
Table of Contents
What Percentage is 4 of 20? A Deep Dive into Percentage Calculations and Their Applications
What percentage is 4 of 20? The answer is a simple 20%, but this seemingly straightforward question opens a door to a world of practical applications and mathematical concepts crucial for various fields. This article will not only answer the initial question but will also delve into the underlying principles of percentage calculations, explore different methods of solving percentage problems, and showcase the significance of percentages in everyday life and professional settings. This comprehensive guide is perfect for anyone seeking a deeper understanding of percentages, from students mastering basic math to professionals analyzing data.
Understanding Percentages: The Foundation
A percentage is a fraction or ratio expressed as a number out of 100. The word "percent" itself is derived from the Latin "per centum," meaning "out of a hundred." This implies that a percentage represents a portion of a whole, with the whole being considered as 100%. Understanding this fundamental concept is crucial for accurately interpreting and calculating percentages.
Calculating "What Percentage is 4 of 20?"
The simplest method to calculate what percentage 4 represents of 20 involves using the following formula:
(Part / Whole) * 100% = Percentage
In this case:
- Part: 4
- Whole: 20
Substituting these values into the formula:
(4 / 20) * 100% = 20%
Therefore, 4 is 20% of 20.
Alternative Methods for Percentage Calculation
While the above method is the most straightforward, several alternative approaches can be used, each offering a slightly different perspective on the problem:
1. Using Proportions:
Percentage problems can also be solved using proportions. A proportion is a statement that two ratios are equal. We can set up a proportion to solve for the unknown percentage (x):
4/20 = x/100
To solve for x, we cross-multiply:
20x = 400
x = 400 / 20
x = 20%
2. Using Decimal Conversion:
First, convert the fraction 4/20 into a decimal by dividing 4 by 20:
4 ÷ 20 = 0.2
Then, multiply the decimal by 100% to express it as a percentage:
0.2 * 100% = 20%
3. Using a Calculator:
Modern calculators often have a percentage function that simplifies the calculation. Simply input "4 ÷ 20 * 100" and the calculator will directly output 20%.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is a fundamental skill with wide-ranging applications in various aspects of daily life and professional fields:
1. Finance and Budgeting:
- Interest rates: Calculating interest earned on savings accounts or interest paid on loans relies heavily on percentage calculations. Understanding compound interest, which involves calculating interest on both the principal amount and accumulated interest, requires a solid grasp of percentages.
- Discounts and sales: Determining the final price of an item after a discount is applied involves calculating a percentage reduction. For example, a 25% discount on a $100 item means subtracting 25% of $100 ($25) from the original price.
- Taxes: Calculating sales tax, income tax, and other types of taxes often involves working with percentages.
- Investment returns: Assessing the performance of investments requires calculating percentage returns or losses.
2. Data Analysis and Statistics:
- Statistical representation: Percentages are commonly used to represent data in charts and graphs, providing a clear and concise way to visualize proportions and trends.
- Probability and risk assessment: Percentages are essential in calculating probabilities and assessing risks in various fields, including insurance, finance, and healthcare. For example, expressing the probability of an event occurring as a percentage provides a readily understandable measure of likelihood.
- Survey results: Analyzing survey results often involves calculating percentages to represent the proportion of respondents who chose each option.
3. Everyday Life:
- Tip calculations: Calculating a tip in a restaurant involves determining a percentage of the bill.
- Grocery shopping: Comparing prices and unit costs often requires calculating percentages to determine the best value.
- Recipe scaling: Adjusting the quantities of ingredients in a recipe involves calculating percentages to maintain the correct proportions.
Beyond the Basics: More Complex Percentage Problems
While calculating "what percentage is 4 of 20" is a relatively simple problem, percentage calculations can become more complex depending on the context:
1. Finding the Whole Given a Percentage and Part:
For example, if you know that 20% of a number is 4, you can calculate the whole number by setting up the equation:
0.20 * x = 4
x = 4 / 0.20
x = 20
2. Finding the Part Given a Percentage and Whole:
Conversely, if you know the percentage and the whole, you can calculate the part. For instance, to find 20% of 20, you would calculate:
0.20 * 20 = 4
3. Percentage Change:
Calculating percentage change involves finding the difference between two values and expressing this difference as a percentage of the original value. This is useful for tracking growth or decline in various metrics, such as sales, profits, or population. The formula is:
((New Value - Old Value) / Old Value) * 100%
4. Percentage Increase/Decrease:
These calculations are specific instances of percentage change. A percentage increase shows growth, while a percentage decrease shows reduction.
Conclusion: Mastering the Power of Percentages
Understanding percentages is a fundamental skill with far-reaching implications. While the answer to "what percentage is 4 of 20?" is straightforward (20%), the underlying principles and diverse applications are far more extensive. Mastering percentage calculations allows for accurate financial management, effective data analysis, and a better comprehension of the world around us. By understanding the different approaches and variations of percentage problems, you can confidently navigate various real-world situations and unlock the power of percentages in numerous contexts. From calculating discounts to analyzing statistical data, the ability to work with percentages is a valuable asset in both personal and professional endeavors.
Latest Posts
Latest Posts
-
What Percent Is 14 Out Of 20
Apr 19, 2025
-
What Is 3 Percent Of 10000
Apr 19, 2025
-
4 Liters Is How Many Milliliters
Apr 19, 2025
-
Cuanto Es 30 Grados Centigrados En Fahrenheit
Apr 19, 2025
-
22 15 As A Mixed Number
Apr 19, 2025
Related Post
Thank you for visiting our website which covers about What Percentage Is 4 Of 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.