What Percentage Of 50 Is 35
Kalali
Apr 12, 2025 · 5 min read
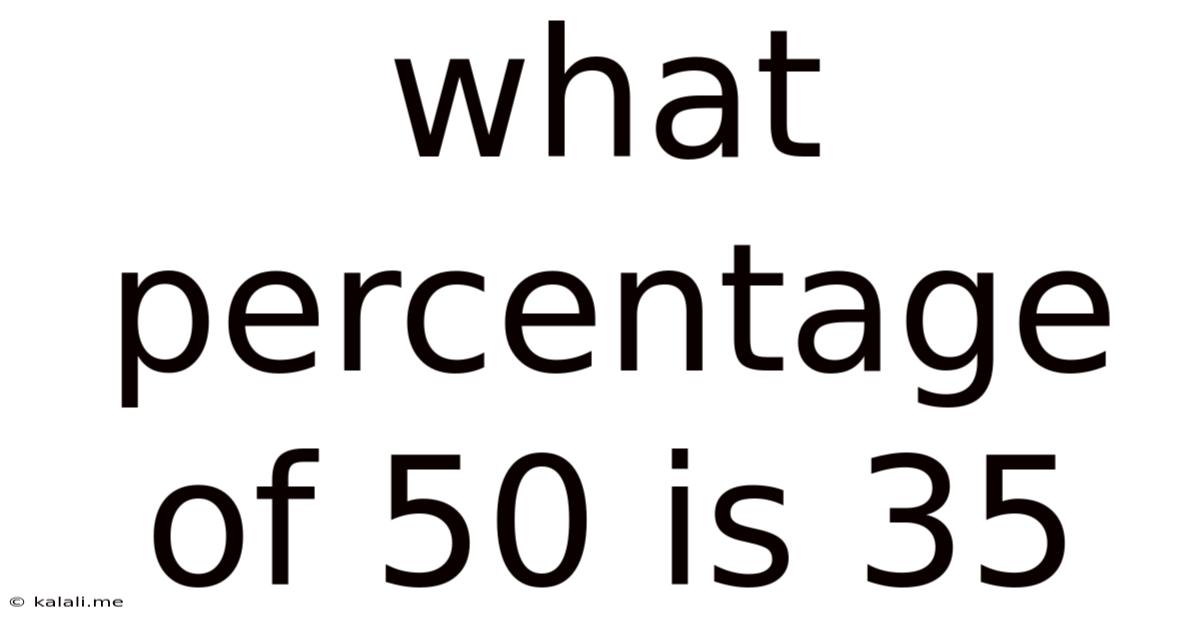
Table of Contents
What Percentage of 50 is 35? A Comprehensive Guide to Percentage Calculations
Finding what percentage one number represents of another is a fundamental mathematical skill with widespread applications in various fields, from finance and budgeting to statistics and data analysis. This article will delve deep into calculating what percentage 35 represents of 50, explaining the process step-by-step and exploring various methods to arrive at the solution. We'll also examine the broader context of percentage calculations and their practical uses. This guide will provide you with a thorough understanding, enabling you to confidently tackle similar percentage problems in the future.
Meta Description: Learn how to calculate what percentage 35 is of 50. This comprehensive guide provides step-by-step instructions, multiple methods, and practical applications of percentage calculations. Master this essential mathematical skill.
Understanding Percentages
Before diving into the specific calculation, let's briefly review the concept of percentages. A percentage is a way of expressing a number as a fraction of 100. The symbol "%" represents "per cent," meaning "out of one hundred." For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2 or 0.5.
Method 1: Using the Formula
The most straightforward method to determine what percentage 35 is of 50 involves using the basic percentage formula:
(Part / Whole) * 100% = Percentage
In this case:
- Part: 35 (the number we want to express as a percentage)
- Whole: 50 (the total number)
Substituting these values into the formula:
(35 / 50) * 100% = 70%
Therefore, 35 is 70% of 50.
Method 2: Proportion Method
Another effective approach is using proportions. We can set up a proportion to solve for the unknown percentage (x):
35/50 = x/100
To solve for x, we cross-multiply:
35 * 100 = 50 * x
3500 = 50x
x = 3500 / 50
x = 70
Therefore, x = 70%, confirming that 35 is 70% of 50.
Method 3: Decimal Conversion
This method involves converting the fraction to a decimal and then multiplying by 100%.
First, express the relationship as a fraction: 35/50
Next, divide the numerator (35) by the denominator (50):
35 ÷ 50 = 0.7
Finally, multiply the decimal by 100% to express it as a percentage:
0.7 * 100% = 70%
Again, we arrive at the answer: 35 is 70% of 50.
Practical Applications of Percentage Calculations
Understanding percentage calculations is crucial in numerous real-world scenarios:
-
Finance: Calculating interest rates, discounts, profit margins, tax rates, and investment returns all rely heavily on percentage calculations. For example, understanding what percentage a down payment represents of the total cost of a house is essential in financial planning. Calculating percentage change in investments is also crucial for portfolio management.
-
Statistics: Percentages are essential in representing and interpreting statistical data. For instance, expressing survey results, demographics, and trends often involves percentages. Analyzing percentage changes in sales figures or market share over time is a vital component of market research.
-
Retail and Sales: Discounts, markups, sales tax, and profit margins are all calculated using percentages. Retailers use percentages to determine pricing strategies and analyze sales performance. Understanding percentage discounts is key for consumers to make informed purchasing decisions.
-
Science and Engineering: Percentages are frequently used to express concentrations, efficiencies, and error margins in scientific experiments and engineering calculations. For example, expressing the percentage of a particular component in a mixture or the percentage efficiency of a machine are common practice.
-
Everyday Life: We encounter percentages daily, from calculating tips in restaurants to understanding nutritional information on food labels. Determining the percentage of a grade earned on a test or the percentage of completion of a project are common occurrences.
More Complex Percentage Problems: Working Backwards
While the example of finding what percentage 35 is of 50 is relatively straightforward, percentage problems can become more complex. Often, you need to work backward to find a missing value. For example:
- Finding the whole: If 30% of a number is 15, what is the number?
To solve this, you would set up the equation:
0.30 * x = 15
x = 15 / 0.30
x = 50
- Finding the part: What is 25% of 80?
This can be solved using the formula:
0.25 * 80 = 20
These examples demonstrate the versatility of percentage calculations and their application in solving various mathematical problems.
Avoiding Common Mistakes in Percentage Calculations
Several common errors can arise when working with percentages. Here are some points to remember:
-
Confusing Part and Whole: Ensure you correctly identify the part and the whole when using the percentage formula. The part is the number you want to express as a percentage of the whole, which is the total amount.
-
Incorrect Decimal Conversion: When converting percentages to decimals, remember to divide by 100. For instance, 70% is equal to 0.70, not 7.0.
-
Rounding Errors: Be mindful of rounding errors, especially when dealing with multiple calculations involving percentages. Rounding intermediate results can lead to inaccuracies in the final answer. It’s often best to retain more decimal places during calculations and round only at the final step.
-
Using the Wrong Formula: Always double-check that you are applying the correct formula based on the specific type of percentage problem you are trying to solve.
Conclusion: Mastering Percentage Calculations
Understanding how to calculate percentages is a valuable skill with numerous applications in various fields. The examples presented in this article, including the detailed explanation of determining what percentage 35 is of 50, illustrate the different methods and underlying principles involved. By mastering these techniques and avoiding common pitfalls, you can confidently tackle a wide range of percentage problems and utilize this knowledge in both academic and professional settings. The ability to perform these calculations accurately and efficiently will significantly enhance your analytical and problem-solving skills. Remember to practice regularly to solidify your understanding and improve your speed and accuracy.
Latest Posts
Latest Posts
-
Number Of Valence Electrons In Al
Apr 18, 2025
-
What Role Does Cellular Respiration Play In The Water Cycle
Apr 18, 2025
-
36 Is What Percent Of 80
Apr 18, 2025
-
32 Is What Percent Of 80
Apr 18, 2025
-
1 4 Inch Equals How Many Mm
Apr 18, 2025
Related Post
Thank you for visiting our website which covers about What Percentage Of 50 Is 35 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.