30 Is What Percent Of 600
Kalali
Apr 22, 2025 · 5 min read
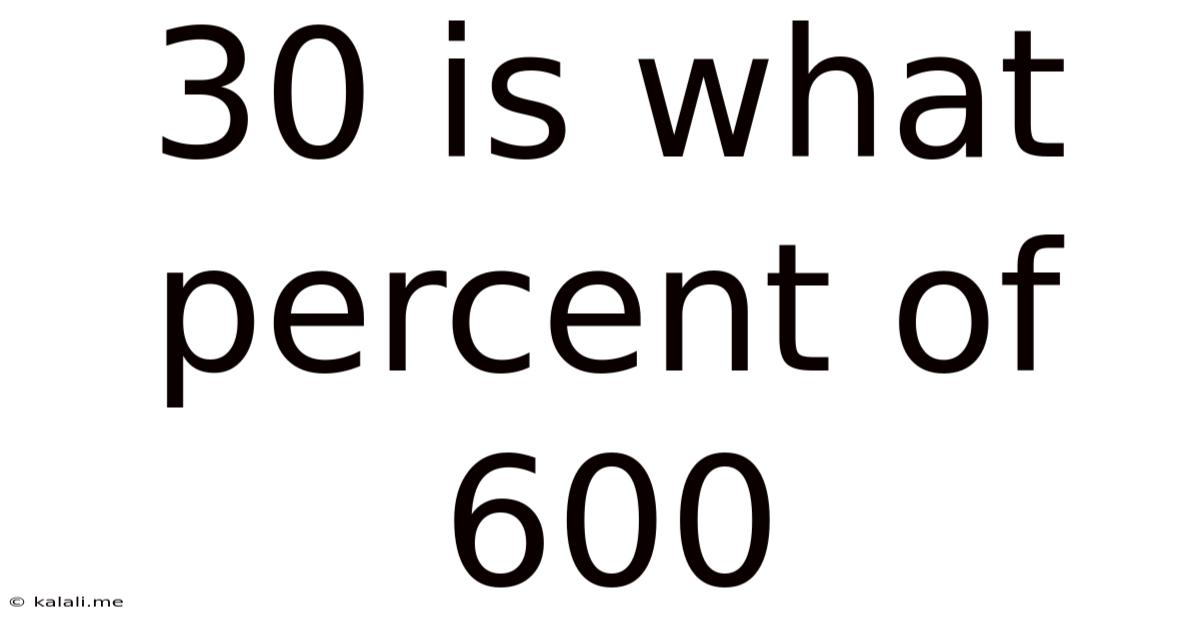
Table of Contents
30 is What Percent of 600? A Comprehensive Guide to Percentage Calculations
This seemingly simple question – "30 is what percent of 600?" – opens the door to a deeper understanding of percentage calculations, a fundamental skill in numerous fields, from finance and budgeting to data analysis and scientific research. This comprehensive guide will not only answer the question directly but also explore the underlying concepts, provide multiple solution methods, and demonstrate the practical applications of percentage calculations.
Meta Description: Learn how to calculate percentages effectively. This guide provides multiple methods to solve "30 is what percent of 600?", explains the underlying concepts, and explores real-world applications of percentage calculations.
Understanding Percentages: The Basics
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred." For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2. Understanding this fundamental concept is crucial for all percentage calculations.
Percentages are used extensively because they provide a standardized way to compare different quantities. Whether you're comparing sales figures, calculating discounts, or analyzing survey results, percentages offer a clear and concise representation of proportions.
Method 1: Using the Percentage Formula
The most straightforward method to solve "30 is what percent of 600?" is by using the basic percentage formula:
(Part / Whole) x 100 = Percentage
In this case:
- Part: 30 (the number we're considering as a portion of the whole)
- Whole: 600 (the total amount)
Substituting these values into the formula:
(30 / 600) x 100 = 5%
Therefore, 30 is 5% of 600.
Method 2: Setting up a Proportion
Another effective approach involves setting up a proportion. A proportion is an equation stating that two ratios are equal. We can represent the problem as:
30 / 600 = x / 100
Where 'x' represents the unknown percentage. To solve for x, we cross-multiply:
30 * 100 = 600 * x
3000 = 600x
x = 3000 / 600
x = 5
Again, this confirms that 30 is 5% of 600.
Method 3: Using Decimal Conversion
This method involves converting the percentage to a decimal and then performing a simple multiplication. To find what percent 30 is of 600, we can set up the equation:
x * 600 = 30
To solve for x (the decimal equivalent of the percentage), we divide both sides by 600:
x = 30 / 600
x = 0.05
To convert this decimal to a percentage, we multiply by 100:
0.05 * 100 = 5%
This method reinforces the connection between decimals and percentages.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is essential in a wide range of situations:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns all rely heavily on percentage calculations. Understanding percentage change is crucial for analyzing financial trends. For example, if a stock price increases from $100 to $110, the percentage increase is calculated as ((110-100)/100) * 100 = 10%.
-
Retail: Calculating discounts, sales tax, and markups are fundamental to retail operations. Understanding percentage discounts allows consumers to make informed purchasing decisions. For example, a 20% discount on a $50 item would result in a savings of $10.
-
Data Analysis: Percentages are used extensively in data analysis to represent proportions, trends, and relationships within datasets. For instance, analyzing survey responses often involves calculating the percentage of respondents who chose each option.
-
Science: Percentage calculations are vital in various scientific fields, from chemistry (calculating concentrations) to biology (analyzing population changes) to physics (measuring efficiency).
-
Everyday Life: Percentages are encountered daily, from calculating tips in restaurants to understanding the nutritional content of food to interpreting weather forecasts (e.g., a 30% chance of rain).
Advanced Percentage Calculations: Percentage Increase and Decrease
Beyond the basic percentage calculations, understanding percentage increase and decrease is crucial for analyzing changes over time.
Percentage Increase: This is calculated using the formula:
[(New Value - Old Value) / Old Value] x 100
For example, if a value increases from 50 to 75, the percentage increase is:
[(75 - 50) / 50] x 100 = 50%
Percentage Decrease: This is calculated using a similar formula:
[(Old Value - New Value) / Old Value] x 100
If a value decreases from 100 to 80, the percentage decrease is:
[(100 - 80) / 100] x 100 = 20%
Solving More Complex Percentage Problems
The principles discussed above can be applied to more complex percentage problems. For instance, consider the following:
-
Finding the whole when given the part and percentage: If 15% of a number is 30, what is the number? You would set up the equation: 0.15x = 30, and solve for x.
-
Finding the part when given the whole and percentage: What is 25% of 800? You would simply multiply 800 by 0.25.
-
Calculating successive percentages: If you apply a 10% discount followed by a 5% discount, the total discount is not simply 15%. You need to calculate the discounts sequentially.
Tips for Mastering Percentage Calculations
-
Practice regularly: The key to mastering percentage calculations is consistent practice. Start with simple problems and gradually work your way up to more complex ones.
-
Understand the concepts: Don't just memorize formulas; understand the underlying concepts of ratios, proportions, and fractions.
-
Use different methods: Experiment with different calculation methods to find the one that works best for you.
-
Check your answers: Always double-check your calculations to ensure accuracy.
Conclusion
This comprehensive guide has provided multiple methods for solving "30 is what percent of 600?", demonstrating that the answer is 5%. However, the true value of this exercise extends beyond finding the solution. Understanding percentage calculations is a crucial skill applicable across numerous disciplines and everyday life. By mastering these techniques and understanding the underlying principles, you will enhance your analytical skills and improve your ability to interpret and utilize numerical information effectively. Remember to practice regularly and explore different problem-solving methods to solidify your understanding and build confidence in tackling various percentage-related challenges.
Latest Posts
Latest Posts
-
What Type Of Angle Is A 154 Angle
Apr 23, 2025
-
What Is The Fraction For 0 375
Apr 23, 2025
-
6 Is What Percent Of 30
Apr 23, 2025
-
32 Of 40 Is What Percent
Apr 23, 2025
-
One And A Half Cups Is How Many Ounces
Apr 23, 2025
Related Post
Thank you for visiting our website which covers about 30 Is What Percent Of 600 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.