33 Is What Percent Of 60
Kalali
Apr 06, 2025 · 4 min read
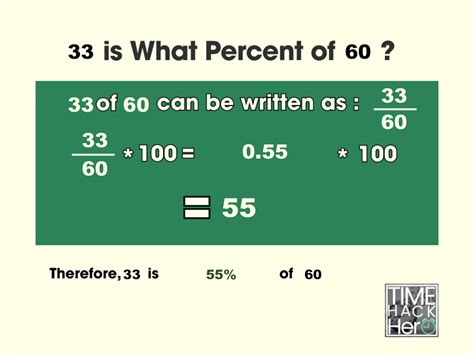
Table of Contents
33 is What Percent of 60? A Comprehensive Guide to Percentage Calculations
This article delves deep into the seemingly simple question: "33 is what percent of 60?" While the answer might seem readily calculable, understanding the underlying principles of percentage calculations is crucial for various applications in daily life, academics, and professional settings. We will not only solve this specific problem but also explore the broader context of percentage calculations, offering practical examples and different methods to tackle similar problems. We'll cover everything from the basic formula to advanced applications and troubleshooting common mistakes.
Understanding Percentages
Before diving into the calculation, let's solidify our understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" literally means "out of one hundred" ("per cent" in Latin). Therefore, 50% means 50 out of 100, which simplifies to ½ or 0.5.
This fundamental understanding forms the bedrock of all percentage calculations. We use percentages to express proportions, changes, and comparisons across diverse fields. From calculating discounts in a store to understanding economic growth rates, percentages are an indispensable tool for interpreting data and making informed decisions.
Calculating "33 is What Percent of 60?" - The Basic Method
The most straightforward approach involves using the basic percentage formula:
(Part / Whole) * 100% = Percentage
In our case:
- Part: 33
- Whole: 60
Substituting these values into the formula:
(33 / 60) * 100% = 55%
Therefore, 33 is 55% of 60.
This method is simple, efficient, and easily adaptable to various percentage problems.
Alternative Methods for Solving Percentage Problems
While the basic formula is sufficient for most scenarios, exploring alternative methods enhances understanding and problem-solving skills. Here are a few alternatives:
Method 2: Using Proportions
This method leverages the concept of equivalent ratios. We can set up a proportion:
33/60 = x/100
Where 'x' represents the unknown percentage. To solve for 'x', we cross-multiply:
60x = 3300
x = 3300 / 60
x = 55
Therefore, 33 is 55% of 60. This method reinforces the relationship between fractions and percentages.
Method 3: Decimal Conversion
This method involves converting the fraction to a decimal and then multiplying by 100%:
33 / 60 = 0.55
0.55 * 100% = 55%
This approach is particularly useful when dealing with fractions that are easily convertible to decimals. It highlights the connection between decimals, fractions, and percentages.
Practical Applications of Percentage Calculations
Percentage calculations are ubiquitous, finding applications in numerous aspects of life:
- Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns.
- Retail: Determining discounts, sales tax, and markups on products.
- Science: Expressing experimental results, error margins, and statistical data.
- Education: Calculating grades, test scores, and performance metrics.
- Everyday Life: Determining tips, comparing prices, understanding nutritional information on food labels.
Solving Similar Percentage Problems
Now that we've tackled "33 is what percent of 60?", let's consider similar problems and how to approach them systematically:
Example 1: What is 20% of 80?
Using the basic formula: (20/100) * 80 = 16
Example 2: 15 is what percent of 75?
Using the basic formula: (15/75) * 100% = 20%
Example 3: 40 is 25% of what number?
This problem requires a slight modification of the formula:
40 = (25/100) * x
Solving for x: x = 40 / (25/100) = 160
Common Mistakes and How to Avoid Them
Several common mistakes can occur during percentage calculations:
- Incorrect Formula Application: Ensuring you use the correct formula (Part/Whole * 100%) is critical.
- Decimal Errors: Carefully manage decimal points during calculations to avoid errors in the final answer.
- Unit Confusion: Always ensure consistent units when dealing with percentages and related quantities.
- Misinterpreting the Question: Clearly understand what the question is asking before applying any formula.
Advanced Percentage Calculations
Beyond the basic calculations, several advanced concepts extend the applications of percentages:
- Percentage Change: Calculating the increase or decrease in a quantity expressed as a percentage.
- Compound Interest: Calculating interest earned on both principal and accumulated interest over time.
- Percentage Points: Distinguishing percentage change from percentage points, a crucial aspect in statistical analysis.
Conclusion
The seemingly simple question, "33 is what percent of 60?", serves as a springboard to exploring the versatile world of percentage calculations. Mastering these calculations equips you with a valuable skill applicable across various fields and daily life situations. Remember the basic formula, explore alternative methods, understand potential errors, and delve into more advanced concepts to become proficient in this crucial mathematical skill. By applying these principles and practicing regularly, you can confidently tackle any percentage problem that comes your way. The ability to perform percentage calculations efficiently and accurately is a highly valuable asset in both personal and professional contexts.
Latest Posts
Latest Posts
-
How Many Neutrons Does Silver Have
Apr 07, 2025
-
How Many Neutrons Are In Boron
Apr 07, 2025
-
0 5 And 0 25 Which Is Greater
Apr 07, 2025
-
183 Out Of 200 As A Percentage
Apr 07, 2025
-
How Much Is 14 Inches In Cm
Apr 07, 2025
Related Post
Thank you for visiting our website which covers about 33 Is What Percent Of 60 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.