How To Use Pascal's Triangle To Expand Polynomials
Kalali
Mar 26, 2025 · 5 min read
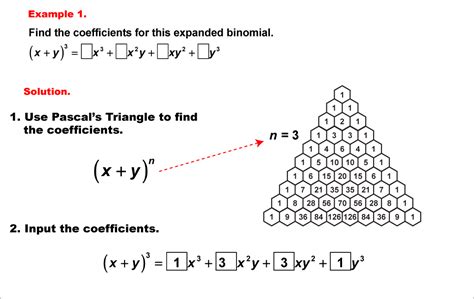
Table of Contents
How to Use Pascal's Triangle to Expand Polynomials
Pascal's Triangle, a deceptively simple arrangement of numbers, offers a powerful shortcut for expanding binomial expressions raised to various powers. Understanding its application significantly simplifies otherwise tedious calculations, especially when dealing with higher exponents. This comprehensive guide explores the intricacies of Pascal's Triangle and how it elegantly solves the challenge of polynomial expansion.
Understanding Pascal's Triangle
Before delving into its application to polynomial expansion, let's understand the structure and generation of Pascal's Triangle. It's a triangular array of numbers where each number is the sum of the two numbers directly above it. The pattern begins with a '1' at the apex, and each subsequent row is built upon the previous one.
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
1 10 45 120 210 252 210 120 45 10 1
Notice the symmetry? Each row is a palindrome, reading the same forwards and backwards. This inherent symmetry is a key feature that simplifies calculations in binomial expansion. Each row, starting from the top, represents the coefficients for a binomial expansion raised to the power of n, where n is the row number (starting with n=0).
Connecting Pascal's Triangle to Binomial Expansion
A binomial is an algebraic expression consisting of two terms, typically represented as (a + b). Expanding (a + b)ⁿ for larger values of 'n' can become extremely complex using traditional multiplication methods. This is where Pascal's Triangle emerges as a powerful tool.
Let's examine how it works:
- Row 0 (n=0): (a + b)⁰ = 1. The single '1' in row 0 reflects this.
- Row 1 (n=1): (a + b)¹ = a + b. The '1 1' in row 1 corresponds to the coefficients of 'a' and 'b'.
- Row 2 (n=2): (a + b)² = a² + 2ab + b². The '1 2 1' in row 2 represents the coefficients of a², 2ab, and b².
- Row 3 (n=3): (a + b)³ = a³ + 3a²b + 3ab² + b³. Observe the correspondence with '1 3 3 1'.
The pattern continues for higher powers of 'n'. The numbers in each row of Pascal's Triangle directly represent the coefficients in the expanded form of (a + b)ⁿ.
Expanding Polynomials using Pascal's Triangle: A Step-by-Step Guide
Let's solidify this understanding with a detailed walkthrough. Suppose we want to expand (x + 2y)⁴.
Step 1: Identify the Row
The exponent is 4, so we need the 5th row of Pascal's Triangle (remembering that the top row is row 0). This row is: 1 4 6 4 1
Step 2: Apply the Coefficients
These numbers will be the coefficients of our expanded polynomial.
Step 3: Determine the Exponents
The exponents of 'x' will descend from 4 to 0, while the exponents of '2y' will ascend from 0 to 4. This ensures that the sum of the exponents in each term always equals 4 (the original exponent).
Step 4: Combine and Simplify
Now, we combine the coefficients, the descending exponents of 'x', and the ascending exponents of '2y':
1*(x⁴)(2y)⁰ + 4(x³)(2y)¹ + 6(x²)(2y)² + 4(x¹)(2y)³ + 1(x⁰)*(2y)⁴
Simplifying this expression, we get:
x⁴ + 8x³y + 24x²y² + 32xy³ + 16y⁴
Therefore, the expansion of (x + 2y)⁴ is x⁴ + 8x³y + 24x²y² + 32xy³ + 16y⁴.
Handling Binomials with Subtraction
Pascal's Triangle also efficiently expands binomials with subtraction. The only difference is that the terms alternate in sign. Consider (a - b)ⁿ. The coefficients remain the same, but the signs alternate: positive, negative, positive, negative, and so on.
Let's expand (x - y)³:
Row 3 of Pascal's Triangle is: 1 3 3 1
The expansion becomes:
1*(x³) - 3*(x²)(y) + 3(x)(y²) - 1(y³) = x³ - 3x²y + 3xy² - y³
Advanced Applications and Considerations
Pascal's Triangle's utility extends beyond simple binomial expansions. It finds applications in:
- Probability: Calculating probabilities in binomial distributions.
- Combinatorics: Determining combinations (choosing 'k' items from a set of 'n' items). The numbers in Pascal's Triangle directly represent binomial coefficients, often written as "n choose k" or ⁿCₖ.
- Calculus: Approximating functions using Taylor series expansions.
Limitations and Alternatives
While Pascal's Triangle provides an elegant method for expanding binomials, it does have limitations:
- Higher Exponents: For very high exponents, generating the necessary row of Pascal's Triangle can become cumbersome.
- Multinomials: Pascal's Triangle directly handles only binomials (two terms). Expanding multinomials (three or more terms) requires more sophisticated techniques.
For higher-order polynomials or multinomials, the binomial theorem, which generalizes the concept of Pascal's Triangle, provides a more efficient and systematic approach. However, for relatively low exponents, Pascal's Triangle offers a clear and intuitive way to expand binomials.
Conclusion: Mastering Polynomial Expansion
Mastering polynomial expansion is crucial in various mathematical fields. Pascal's Triangle offers an accessible and efficient method, particularly for lower-order expansions. By understanding its structure, applying its coefficients correctly, and handling alternating signs in subtraction, you can significantly simplify the process. Remember that while Pascal's Triangle serves as a valuable tool, other methods, such as the binomial theorem, are better suited for higher-order polynomials and more complex scenarios. The combination of a clear understanding of Pascal's Triangle and the broader mathematical concepts related to binomial expansion will equip you with powerful techniques to tackle a wide range of polynomial problems. Remember to practice frequently to solidify your understanding and improve your efficiency in expanding polynomials.
Latest Posts
Latest Posts
-
How To Recognize A Redox Reaction
Mar 29, 2025
-
95 Degrees Fahrenheit Converted To Celsius
Mar 29, 2025
-
Whats 2 1 2 As A Decimal
Mar 29, 2025
-
31 Degrees C Is What In F
Mar 29, 2025
-
5 Feet 8 Inches In Meters
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about How To Use Pascal's Triangle To Expand Polynomials . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
