What Is A 14/15 In Percentage
Kalali
Apr 25, 2025 · 5 min read
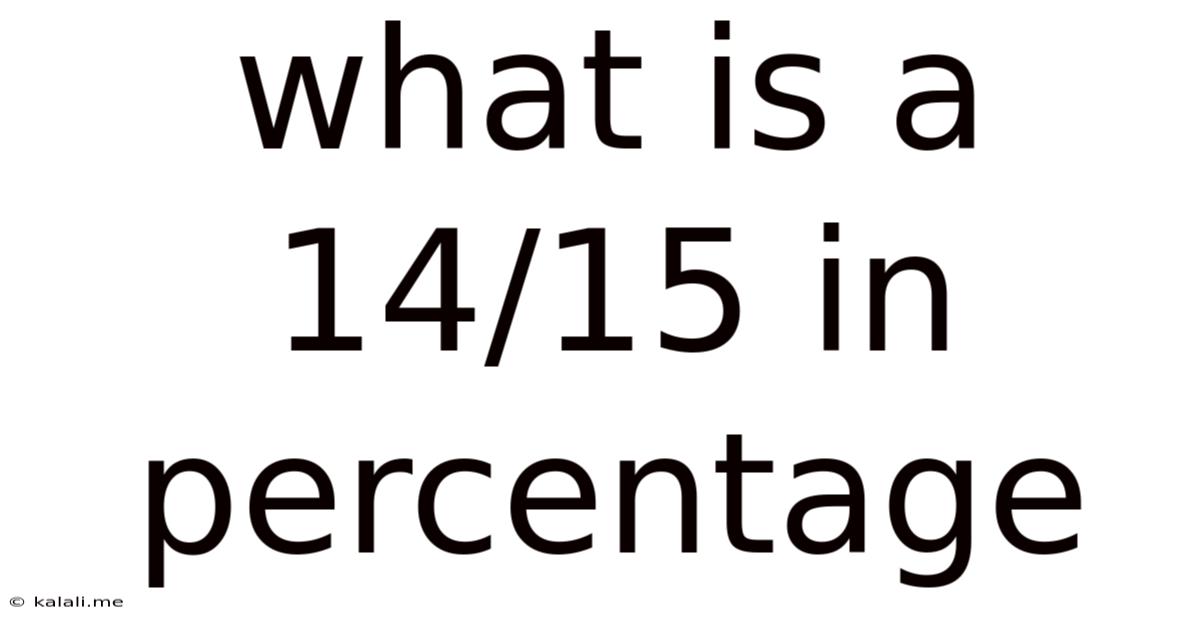
Table of Contents
What is a 14/15 in Percentage? A Comprehensive Guide to Fraction-to-Percentage Conversions
Understanding how to convert fractions to percentages is a fundamental skill applicable across various fields, from academic assessments to financial calculations. This comprehensive guide will delve into the specifics of converting 14/15 into a percentage, explaining the process step-by-step and providing broader context on fraction-to-percentage conversions. This guide will also explore practical applications and address common misconceptions. By the end, you'll not only know the percentage equivalent of 14/15 but also understand the underlying principles and be able to confidently perform similar conversions.
What is a Percentage?
Before we dive into the conversion, let's establish a clear understanding of percentages. A percentage is a way of expressing a number as a fraction of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of one hundred." Therefore, 50% means 50 out of 100, or 50/100, which simplifies to 1/2. Percentages are widely used to represent proportions, rates, and changes, making them a versatile tool in various applications.
Converting Fractions to Percentages: The General Method
The core principle of converting a fraction to a percentage involves expressing the fraction as an equivalent fraction with a denominator of 100. This can be achieved through several methods, but the most common and generally applicable approach is as follows:
-
Divide the numerator by the denominator: This step converts the fraction into a decimal. For example, with the fraction 14/15, we divide 14 by 15.
-
Multiply the decimal by 100: This step transforms the decimal into a percentage. Multiplying by 100 is equivalent to moving the decimal point two places to the right.
Calculating 14/15 as a Percentage
Let's apply this method to our specific fraction, 14/15:
-
Division: 14 ÷ 15 = 0.93333... (the 3s repeat infinitely)
-
Multiplication: 0.93333... × 100 = 93.333...%
Therefore, 14/15 is approximately 93.33%. The repeating decimal indicates that the percentage is not perfectly precise, but 93.33% provides a sufficiently accurate representation for most purposes. Rounding to two decimal places is standard practice in many contexts.
Alternative Methods for Fraction-to-Percentage Conversion
While the division-and-multiplication method is the most common, there are alternative approaches:
-
Finding an equivalent fraction with a denominator of 100: In some cases, you might be able to directly find an equivalent fraction with 100 as the denominator. However, this is often not practical, especially with fractions that don't have easily identifiable factors of 100. For example, finding an equivalent fraction for 14/15 with a denominator of 100 is complex.
-
Using a calculator: Calculators are invaluable tools for fraction-to-percentage conversions, especially with more complex fractions or those involving repeating decimals. Most calculators have a percentage function that simplifies the process.
Practical Applications of Percentage Conversions
Understanding fraction-to-percentage conversions is crucial in a wide array of practical scenarios:
-
Academic Performance: Grading systems often use percentages to represent student performance. Converting a fraction of correctly answered questions to a percentage gives a clear indication of achievement. For example, a student scoring 14 out of 15 on a test achieved 93.33%.
-
Financial Calculations: Percentages are essential in finance for calculating interest rates, discounts, taxes, and profit margins. Understanding these conversions allows for accurate financial analysis and decision-making. For instance, a 15% discount on a $100 item means a $15 reduction in price.
-
Data Analysis and Statistics: Percentages are widely used in data analysis and statistical reporting to represent proportions, trends, and changes. Converting fractions to percentages facilitates clear communication and interpretation of data. For example, representing survey results as percentages simplifies the understanding of the overall findings.
-
Everyday Life: Percentages are encountered frequently in everyday life, such as sales promotions, nutritional information on food labels, and weather forecasts. Understanding these conversions improves comprehension and effective decision-making.
Common Misconceptions about Percentages
-
Confusing Fractions with Percentages: While related, fractions and percentages are distinct ways of representing proportions. A fraction expresses a part of a whole as a ratio of two numbers, whereas a percentage expresses the same proportion as a fraction of 100.
-
Incorrect Rounding: When converting fractions to percentages, improper rounding can lead to inaccuracies. It’s important to understand the level of precision required and round accordingly. For example, rounding 93.333...% to 93% is a significant difference in some contexts.
-
Ignoring Repeating Decimals: It is crucial to acknowledge the presence of repeating decimals. While simplifying the answer is often necessary, understanding that the decimal value continues infinitely is important, particularly in scenarios demanding high precision.
Advanced Applications: Understanding Percentage Increase and Decrease
Beyond simple conversion, percentage calculations extend to understanding percentage change. This involves calculating the percentage increase or decrease between two values. The formula for percentage change is:
(New Value - Old Value) / Old Value * 100%
For example, if a value increases from 10 to 14, the percentage increase is:
(14 - 10) / 10 * 100% = 40%
Conclusion: Mastering Fraction-to-Percentage Conversions
The conversion of 14/15 to a percentage, approximately 93.33%, highlights the importance of understanding fraction-to-percentage conversions. This fundamental skill has broad applications across various domains, from academic achievements to financial calculations and data analysis. By mastering this skill, individuals enhance their ability to interpret data, make informed decisions, and effectively communicate quantitative information. Remember to always consider the context and required precision when performing these conversions and rounding your final answer. This understanding lays a solid foundation for more advanced mathematical and statistical concepts.
Latest Posts
Latest Posts
-
33 8 As A Mixed Number
Apr 25, 2025
-
Is A Grasshopper A Primary Consumer
Apr 25, 2025
-
65 Out Of 75 As A Percentage
Apr 25, 2025
-
What Is 2 75 In A Fraction
Apr 25, 2025
-
What Percent Of 40 Is 3
Apr 25, 2025
Related Post
Thank you for visiting our website which covers about What Is A 14/15 In Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.