What Percent Of 12 Is 18
Kalali
Apr 26, 2025 · 5 min read
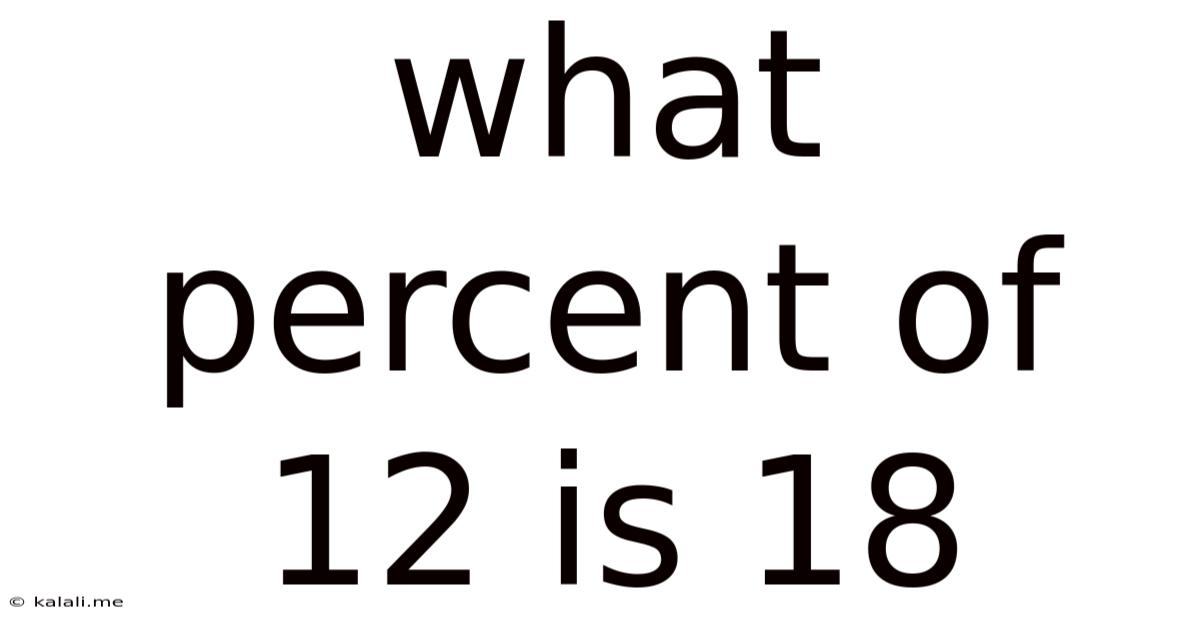
Table of Contents
What Percent of 12 is 18? Unpacking Percentage Calculations and Their Applications
This seemingly simple question – "What percent of 12 is 18?" – opens the door to a broader understanding of percentage calculations, their practical applications, and how to solve similar problems with confidence. While the answer might seem counterintuitive at first glance (since 18 is larger than 12), understanding the underlying mathematical principles reveals a straightforward solution and highlights the versatility of percentages in various contexts. This article will not only provide the solution but also delve into the methodology, explore related concepts, and demonstrate the real-world applications of percentage calculations.
Meta Description: Learn how to calculate percentages, understand the concept of "What percent of 12 is 18?", and discover practical applications of percentage calculations in everyday life and various fields. Master percentage problems with clear explanations and examples.
Understanding the Fundamentals of Percentages
A percentage is a way of expressing a number as a fraction of 100. The symbol "%" represents "per cent," meaning "out of one hundred." For instance, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5. Percentages are widely used to represent proportions, rates, and changes in various contexts.
Solving "What Percent of 12 is 18?"
The question "What percent of 12 is 18?" can be expressed as an algebraic equation:
x% * 12 = 18
To solve for x, we follow these steps:
-
Convert the percentage to a decimal: x% can be written as x/100.
-
Substitute: The equation becomes (x/100) * 12 = 18
-
Simplify: 12x/100 = 18
-
Isolate x: Multiply both sides by 100: 12x = 1800
-
Solve for x: Divide both sides by 12: x = 1800/12 = 150
Therefore, 150% of 12 is 18. This result makes sense because 18 is larger than 12, indicating a percentage greater than 100%.
Alternative Methods for Solving Percentage Problems
Several other methods can be used to solve percentage problems, offering flexibility depending on the specific problem and individual preference. Here are a couple of alternative approaches:
-
Using Proportions: We can set up a proportion: x/100 = 18/12. Cross-multiplying gives 12x = 1800, leading to the same solution: x = 150.
-
Using the Formula: The general formula for percentage problems is: (Part/Whole) * 100 = Percentage. In this case, the part is 18, and the whole is 12. So, (18/12) * 100 = 150%.
Practical Applications of Percentage Calculations
Percentage calculations are fundamental in numerous real-world scenarios across various disciplines. Here are some examples:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and returns on investment all rely heavily on percentage calculations. Understanding percentages is crucial for making informed financial decisions, budgeting effectively, and managing personal finances.
-
Business and Economics: Analyzing market share, growth rates, inflation rates, unemployment rates, and various economic indicators involves extensive use of percentages. Businesses use percentages to track sales, costs, and profits, make pricing decisions, and assess the performance of their operations.
-
Science: Scientific research often involves expressing data as percentages. For instance, researchers might report the percentage of participants in a study who exhibited a particular outcome or the percentage of a substance in a mixture.
-
Everyday Life: We encounter percentages daily, from calculating tips in restaurants to understanding sales discounts in stores, determining the nutritional content of food, and interpreting statistical data in news reports.
Understanding Percentages Greater Than 100%
The result of 150% in this problem highlights an important concept: percentages can be greater than 100%. This simply means that the "part" is larger than the "whole." This often occurs when comparing changes or growth over time, such as population growth, economic expansion, or increases in sales figures.
For example, if a company's sales increased from $12 million to $18 million, the percentage increase would be 150% – a significant growth exceeding the initial value.
Working with Different Percentage Problems
Let's explore a few variations to solidify understanding:
Example 1: What is 25% of 80?
Using the formula: (25/100) * 80 = 20
Example 2: 15 is what percent of 60?
(15/60) * 100 = 25%
Example 3: 30 is 75% of what number?
Let x be the number: 0.75x = 30; x = 30/0.75 = 40
Advanced Percentage Calculations and Applications
While the basic principles are relatively straightforward, more complex percentage calculations involve multiple steps or the application of percentage change formulas. These are often seen in compound interest calculations, analyzing percentage increases or decreases over multiple periods, and scenarios involving discounts and taxes applied sequentially.
-
Compound Interest: Compound interest calculates interest not only on the principal amount but also on accumulated interest from previous periods. Understanding compound interest is crucial for making informed decisions regarding savings, investments, and loans. The formula involves exponential growth, highlighting the power of compounding over time.
-
Percentage Change: Calculating percentage change involves determining the difference between two values and expressing that difference as a percentage of the original value. This is used extensively in tracking economic indicators, market trends, and scientific measurements. The formula usually involves subtracting the initial value from the final value, dividing the result by the initial value, and multiplying by 100.
-
Sequential Discounts and Taxes: When multiple discounts or taxes are applied sequentially, the calculations can become more complex. It's crucial to understand the order of operations and the impact of each discount or tax on the remaining value.
Mastering Percentage Calculations: Tips and Strategies
-
Practice Regularly: The key to mastering percentage calculations is consistent practice. Work through various examples, including those with percentages greater than 100%.
-
Understand the Concepts: Don't just memorize formulas; understand the underlying concepts of ratios, proportions, and fractions.
-
Use Visual Aids: Diagrams, charts, and graphs can help visualize percentage relationships and make calculations easier to understand.
-
Utilize Calculators: While understanding the principles is essential, calculators can be useful for performing calculations quickly and accurately, especially for more complex problems.
-
Break Down Complex Problems: When faced with complex percentage calculations, break down the problem into smaller, manageable steps.
In conclusion, while the initial question, "What percent of 12 is 18?", might seem simple, it serves as a gateway to a comprehensive understanding of percentage calculations and their widespread applications. Mastering these concepts empowers you to tackle various real-world problems in finance, business, science, and everyday life with confidence and precision. By applying the methods and strategies discussed in this article, you can confidently approach and solve a wide range of percentage problems. Remember to focus on understanding the underlying principles, practice regularly, and leverage available tools to enhance your proficiency in this essential mathematical skill.
Latest Posts
Latest Posts
-
What Is The Input Of Photosynthesis
Apr 27, 2025
-
8 Is What Percent Of 60
Apr 27, 2025
-
10 Out Of 17 As A Percentage
Apr 27, 2025
-
100 Is What Percent Of 500
Apr 27, 2025
-
Does 4 Cups Equal A Quart
Apr 27, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 12 Is 18 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.