Which Best Describes A Reference Frame
Kalali
Mar 28, 2025 · 7 min read
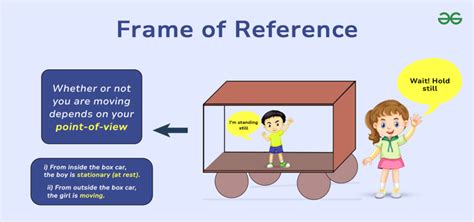
Table of Contents
Which Best Describes a Reference Frame? A Deep Dive into Frames of Reference in Physics
Understanding reference frames is fundamental to grasping many concepts in physics, from Newtonian mechanics to Einstein's theories of relativity. While the concept might seem initially abstract, it's crucial for accurately describing motion and interactions within the universe. This article will delve deep into what constitutes a reference frame, exploring its various types, applications, and the importance of choosing the appropriate frame for a given problem. We'll unravel the intricacies, clarifying common misconceptions and highlighting the practical implications of this essential physics concept.
What is a Reference Frame?
At its core, a reference frame is a coordinate system used to describe the position and motion of objects in space and time. It's essentially a perspective from which we observe and measure events. Imagine yourself watching a car drive past. Your position, the point from which you're observing the car, constitutes your reference frame. Someone else standing further down the road will have a different reference frame, observing the same car's motion but from a different perspective.
A complete reference frame includes:
- A coordinate system: This allows us to specify the location of objects using coordinates (e.g., x, y, z in three-dimensional space). Different coordinate systems exist, such as Cartesian, polar, and spherical coordinates, each offering advantages depending on the symmetry of the problem.
- A time coordinate: This specifies the time at which events occur, enabling us to describe the motion of objects as a function of time. The choice of time coordinate is crucial, especially in relativistic physics, where simultaneity is relative.
- An observer: The observer is the entity within the reference frame who makes measurements and records observations. The observer's perspective significantly influences the measurement of various physical quantities.
The importance of specifying a reference frame cannot be overstated. The description of motion is always relative to a chosen reference frame. An object may appear stationary in one frame but moving in another.
Types of Reference Frames
Reference frames can be categorized in several ways, depending on their properties and characteristics. Here are some key distinctions:
1. Inertial vs. Non-Inertial Reference Frames:
This is perhaps the most important distinction.
-
Inertial Reference Frames: An inertial reference frame is one in which Newton's first law of motion holds true. In simpler terms, an object at rest remains at rest, and an object in motion continues in motion with a constant velocity unless acted upon by a net external force. In essence, these are frames that are not accelerating. They can be moving at a constant velocity, but not accelerating. A spacecraft drifting freely in space, far from any gravitational influences, is a good approximation of an inertial frame.
-
Non-Inertial Reference Frames: A non-inertial reference frame is one that is accelerating. This could be due to linear acceleration (like a car speeding up) or rotational acceleration (like a spinning merry-go-round). In non-inertial frames, Newton's first law doesn't hold directly. Fictitious forces, such as the centrifugal force and the Coriolis force, must be introduced to account for the effects of acceleration. For instance, the feeling of being pushed outward when riding a merry-go-round is a consequence of the centrifugal force, a fictitious force arising from the rotating reference frame.
2. Galilean vs. Newtonian Reference Frames:
While often used interchangeably, there's a subtle difference:
-
Galilean Reference Frames: These are essentially inertial frames under the assumptions of Galilean relativity, where the laws of physics are the same in all inertial frames, and velocities add linearly. This is a good approximation for speeds much smaller than the speed of light.
-
Newtonian Reference Frames: This is a broader term encompassing both inertial and non-inertial frames within the context of Newtonian mechanics. It accounts for the fact that Newton's laws can be applied to non-inertial frames by introducing fictitious forces.
3. Lab Frame vs. Center-of-Mass Frame:
These are often used in specific contexts, especially in collision problems:
-
Lab Frame: This is the reference frame in which the experiment or observation is conducted. It’s often the frame "fixed" to the Earth's surface.
-
Center-of-Mass Frame: This frame is attached to the center of mass of the system being studied. In this frame, the total momentum of the system is always zero. This frame simplifies many calculations, especially in collision problems, as it eliminates the need to account for the overall motion of the system.
The Importance of Choosing the Right Reference Frame
Selecting the appropriate reference frame is crucial for simplifying problem-solving and achieving accurate results. The choice depends heavily on the nature of the problem:
-
Symmetry Considerations: If the problem possesses certain symmetries (e.g., rotational symmetry), choosing a reference frame that reflects this symmetry can significantly simplify the calculations.
-
Minimizing Complexity: Often, choosing an inertial frame minimizes the number of forces to consider, eliminating the need to deal with fictitious forces in non-inertial frames. However, sometimes a non-inertial frame might be more convenient, depending on the specific scenario.
-
Relativistic Effects: In scenarios involving speeds approaching the speed of light, the choice of reference frame becomes even more critical due to the relativistic effects of time dilation and length contraction. Einstein's theory of special relativity dictates that the laws of physics remain the same in all inertial frames, but measurements of time and space differ depending on the observer's relative velocity.
Examples of Reference Frames in Action:
Let's consider a few scenarios to illustrate the significance of reference frames:
-
A person walking on a moving train: Relative to the train, the person's velocity is their walking speed. However, relative to the ground, their velocity is the sum of their walking speed and the train's speed.
-
A projectile launched from a moving platform: The projectile's trajectory will differ depending on whether it is observed from the platform's reference frame or from a stationary frame on the ground.
-
A satellite orbiting Earth: The satellite's motion is described differently depending on whether we use a reference frame fixed to Earth or a frame fixed to the Sun. Earth's rotation needs to be considered if using an Earth-fixed frame, but not if using a Sun-fixed frame.
Reference Frames and Relativity:
The concept of reference frames plays a pivotal role in Einstein's theories of relativity.
-
Special Relativity: Special relativity deals with inertial reference frames and introduces the concept of the constancy of the speed of light in all inertial frames. This has profound implications for our understanding of space, time, and simultaneity. Events that are simultaneous in one inertial frame may not be simultaneous in another.
-
General Relativity: General relativity extends the concept of reference frames to include accelerated and gravitational fields. It introduces the equivalence principle, stating that the effects of gravity are indistinguishable from the effects of acceleration. This leads to the concept of curved spacetime, where the geometry of spacetime is influenced by the presence of mass and energy. The choice of reference frame in general relativity becomes much more complex due to the curvature of spacetime.
Common Misconceptions about Reference Frames:
-
Absolute Motion: There's no such thing as absolute motion. Motion is always relative to a chosen reference frame.
-
The Earth is a perfect inertial frame: The Earth is not a perfect inertial frame due to its rotation and revolution around the Sun. However, for many everyday situations, it's a reasonable approximation of an inertial frame.
-
Fictitious forces are "real": Fictitious forces are not real forces in the sense that they are not caused by physical interactions between objects. They are artifacts of the choice of a non-inertial reference frame.
Conclusion:
Understanding reference frames is crucial for accurately describing motion and interactions in physics. The choice of reference frame profoundly influences the observed motion of objects, the appearance of forces, and the interpretation of physical phenomena. From simple everyday observations to the complexities of Einstein's theories, the concept of the reference frame remains a fundamental pillar in our understanding of the universe. Mastering this concept is essential for anyone seeking a deeper appreciation of physics. Choosing the right reference frame not only simplifies calculations but also ensures accurate and meaningful interpretation of physical events. Remember the key distinctions between inertial and non-inertial frames, and always consider the implications of your chosen perspective. With practice and careful consideration, navigating the world of reference frames will become second nature.
Latest Posts
Latest Posts
-
What Is The Least Common Multiple Of 7 And 9
Mar 31, 2025
-
12 Is What Percent Of 60
Mar 31, 2025
-
Compare And Contrast The Two Types Of Fermentation
Mar 31, 2025
-
How Much Is 120 Ounces Of Water
Mar 31, 2025
-
What Is 6 15 As A Percent
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Which Best Describes A Reference Frame . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
